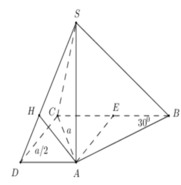
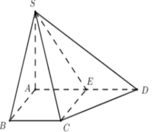
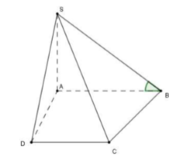
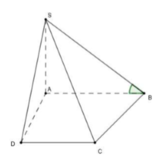
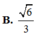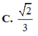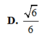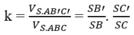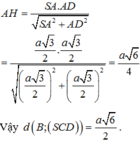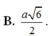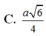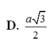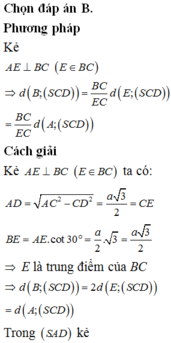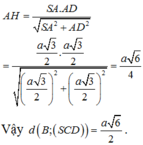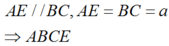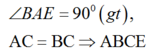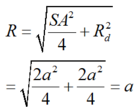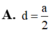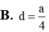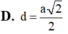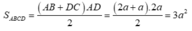Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, A D = 3 a , B C = C D = 4 a ; cạnh bên SA vuông góc với đáy và S A = a 3 . Gọi M là điểm nằm trên cạnh AD sao cho A M = a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cos α bằng