Giá trị lớn nhất của biểu thức A= 4-√x là:
A. 4 B.0 C. -4 D. Kết quả khác
Giá trị lớn nhất của biểu thức: \(P=-x+4\sqrt{x}\) là:
A. 1
B. 2
C. 3
D. 4
\(P=-\left(x-4\sqrt{x}+4\right)+4=-\left(\sqrt{x}-2\right)^2+4\le4\)
\(P_{max}=4\)
a) Tìm giá trị nhỏ nhất của biểu thức: S= \(\dfrac{5x^4+4x^2+10}{x^4+2}\)
b) Tìm giá trị lớn nhất của biểu thức: T=\(\dfrac{2x^4-4x^2+8}{x^4+4}\)
c) Cho a là hằng số và a>0. Tìm giá trị nhỏ nhất của biểu thức: M=\(\dfrac{8y^8+2a\left(y-3\right)^2+2a^2}{4y^8+a^2}\)
Câu 11: Giá trị của biểu thức (x – 2)(x2 + 2x + 4) tại x = - 2 là:
A. -16 B. 0 C. -14 D. 2
Câu 12: Giá trị x thỏa mãn x(x – 2) + x – 2 = 0 là:
A.x=0 B.x=2 C.x=-1; x=2 D.x=0; x=-2
Câu 13: Giá trị x thỏa mãn x(x + 1) - 3.(x+1) = 0 là:
A. x=3 B.x=-1 C.x=3; x=-1 D.x=-3; x=-1
Câu 14: (x – y)2 bằng:
A. x2 + y2 B. (y – x)2 C. y2 – x2 D. x2 – y2
Câu 15: Giá trị nhỏ nhất của đa thức x2 +2x + 5 bằng
A.0 B.1 C.4 D.5
Câu 11: Giá trị của biểu thức (x – 2)(x2 + 2x + 4) tại x = - 2 là:
A. -16 B. 0 C. -14 D. 2
Câu 12: Giá trị x thỏa mãn x(x – 2) + x – 2 = 0 là:
A.x=0 B.x=2 C.x=-1; x=2 D.x=0; x=-2
Câu 13: Giá trị x thỏa mãn x(x + 1) - 3.(x+1) = 0 là:
A. x=3 B.x=-1 C.x=3; x=-1 D.x=-3; x=-1
Câu 14: (x – y)2 bằng:
A. x2 + y2 B. (y – x)2 C. y2 – x2 D. x2 – y2
Câu 15: Giá trị nhỏ nhất của đa thức x2 +2x + 5 bằng
A.0 B.1 C.4 D.5
Giá trị x=.....thì biểu thức D=-1/5(1/4-2x)^2-l8x-1l+2016đạt giá trị lớn nhất. (nhập kết quả dưới dạng số thập phân gọn nhất)
Giá trị x=.....thì biểu thức D=-1/5(1/4-2x)^2-l8x-1l+2016đạt giá trị lớn nhất. (nhập kết quả dưới dạng số thập phân gọn nhất)
Câu 1: Kết quả tìm được của x trong biểu thức x- 3/4= 1/2 là:
A.5/4 . B.-5/4 . C.3/4 . D.6/12 .
câu 21:giá trị của biểu thức A=\(x^2-2x+1tại\) x=1 là:
a.1 b.0 c.2 d.-1
câu 22:kết quả rút gọn phân thức \(\dfrac{x-2}{x\left(2-x\right)}\) (với x\(\ne\) 2 là:
a.x b.\(\dfrac{1}{x}\) c.\(-\dfrac{1}{x}\) d.-x
câu 25.với x=105 thì giá trị của biểu thức:\(x^2-10x+25bằng:\)
a.1000 b.10000 c.1025 d.10025
câu 28.tập hợp các giá trị của x để \(3x^2=2xlà\)
a.\(\left\{0\right\}\) b.\(\left\{\dfrac{3}{2}\right\}\) c.\(\left\{\dfrac{2}{3}\right\}\) d.\(\left\{0;\dfrac{2}{3}\right\}\)
câu 31.khai triển hằng đẳng thức (a-b)\(^3\),ta được.
a.(a-b)(a+b)\(^2\) b.\(a^2-b^2\) c.3a-3b d.\(a^3-3a^2b+3ab^2-b^3\)
câu 33.cho hai đa thức :A=10x\(^2\)+20x+10 và B=x+1.Đa thức du trong phép chia A cho B là:
a.10 b.10(x+1) c.x+1 d.0
câu 37.rút gọn biểu thức (a+b)\(^2-\left(a-b\right)^2\)ta được:
a.\(2b^2\) b.\(2a^2\) c.\(-4ab\) d.4ab
câu 38.kết quả của phép chia \(\left(x^3-1\right):\left(x-1\right)\) bằng:
a.\(x^2+x+1\) b.\(x^2-2x+1\) c.\(x^2+2x+1\) d.\(x^2-x+1\)
câu 40.giá trị của phân thức \(\dfrac{x-1}{2x-6}\)được xác định khi:
a.\(x\ne3\) b.\(x\ne1\) \(c.x\ne-3\) d.\(x\ne0\)
câu 42.tích (3x-5y)(3x+5y) là:
\(a.3x^2-5y^2\) \(b.9x^2+10y^2\) \(c,9x^2-25y^2\) \(d.9x-25y^2\)
câu 43 tích 2x\(^3\)(\(-3x^2+2x-1)là\)
\(a.6x^5+4x^4+2x^3\) b.\(-6x^5+4x^4+2x^3\) c.\(-6x^5+4x^4-2x^3\) d.\(6x^5+4x^4-2x^3\)
câu 44 kết quả đa thức \(6x^2\left(2x-3y\right)-10x\left(2x-3y\right)\) phân tích thành nhân tử được:
a.2x(2x-3y) b.x(2x-3y)(3x-5) c.2x(2x-3y)(3x-5) d.\(5\left(2x-3y\right)\left(3x-5\right)\)
câu 45 chọn câu trả lời đúng :
a.số 1 là phân thức đại số. b.số 0 là phân thức đại số
c.mỗi đa thức là 1 phân thức đại số d.cả A,B,C đều đúng
câu 48 tích (\(7x^2-4x)\left(x-2\right)là\)
a.\(7x^3+18x^2+8x\) b.\(7x^3-18x^2-8x\) c.\(7x^2-18x^2+8\) d.\(7x^3-18x^2+8x\)
câu 49 tích \(2x^3\left(-x^2+2x-4\right)là:\)
a.\(10x^5+15x^4+25x^3\) b.\(-10x^5+5x^4+25x^3\) c.\(-2x^5+4x^4-8x^3\) d.\(2x^5+4x^4-8x^3\)
a) Biểu diễn miền nghiệm D của bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - y \le 6\\2x - y \le 2\\x \ge 0\\y \ge 0\end{array} \right.\)
b) Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F(x;y) = 2x + 3y\) trên miền D.
+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
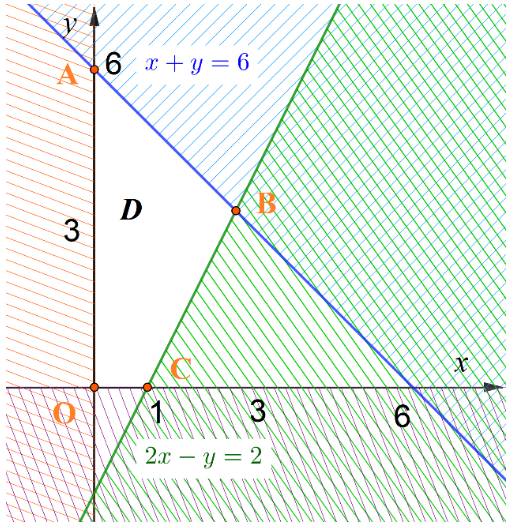
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).
Giá trị x=................ thì biểu thức D= -1/5*(1/4 -2*X)^2-|8*X-1|-2016 đạt giá trị lớn nhất.
(nhập kết quả dưới dạng số thập phân gọn nhất)