Tìm GTLN (Max) và GTNN (Min) của biểu thức y = 3 sin x - 4 cos x ( x ∈ ℝ )
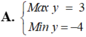
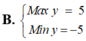
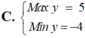
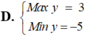
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
A. m a x y = 4 7 , m i n y = - 4 7
B. m a x y = 2 7 7 , m i n y = - 2 7 7
C. m a x y = 7 2 , m i n y = - 2 7
D. m a x y = 2 7 7 , m i n y = - 2 7 7
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là:
A. m i n y = - 3 2 - 1 , m a x y = 3 2 + 1
B. m i n y = - 3 2 - 1 , m a x y = 3 2 - 1
C. m i n y = - 3 2 , m a x y = 3 2 - 1
D. m i n y = - 3 2 - 2 , m a x y = 3 2 - 1
Tìm GTLN (max) và GTNN (min) của y = x + 1 x với x ∈ 3 2 ; 3
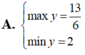
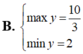
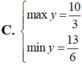
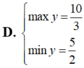
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
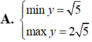
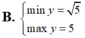
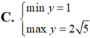
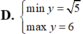
Tìm GTNN và GTLN của hàm số sau:
1.\(y=cosx+cos\left(x-\dfrac{\pi}{3}\right)\)
2.\(y=sin^4x+cos^4x\)
3.\(y=3-2\left|sinx\right|\)
2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$
1.
\(y=\cos x+\cos (x-\frac{\pi}{3})=\cos x+\frac{1}{2}\cos x+\frac{\sqrt{3}}{2}\sin x\)
\(=\frac{3}{2}\cos x+\frac{\sqrt{3}}{2}\sin x\)
\(y^2=(\frac{3}{2}\cos x+\frac{\sqrt{3}}{2}\sin x)^2\leq (\cos ^2x+\sin ^2x)(\frac{9}{4}+\frac{3}{4})\)
\(\Leftrightarrow y^2\leq 3\Rightarrow -\sqrt{3}\leq y\leq \sqrt{3}\)
Vậy $y_{\min}=-\sqrt{3}; y_{max}=\sqrt{3}$
Tìm GTLN, GTNN của các biểu thức sau
1, \(A=sinx-cosx\)
2, \(B=sinx=cosx\)
3, \(C=asinx-bcosx\)
4, \(D=sin^4x-cos^4x\)
\(A=\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\Rightarrow-\sqrt{2}\le A\le\sqrt{2}\)
B ko rõ đề
\(C=\sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}}sinx-\dfrac{b}{\sqrt{a^2+b^2}}cosx\right)\)
Đặt \(\dfrac{a}{\sqrt{a^2+b^2}}=cosy\Rightarrow\dfrac{b}{\sqrt{a^2+b^2}}=siny\)
\(\Rightarrow C=\sqrt{a^2+b^2}\left(sinx.cosy-cosx.siny\right)=\sqrt{a^2+b^2}sin\left(x-y\right)\)
\(\Rightarrow-\sqrt{a^2+b^2}\le C\le\sqrt{a^2+b^2}\)
\(D=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=sin^2x-cos^2x=-cos2x\)
\(\Rightarrow-1\le D\le1\)
Tìm giá trị max, min của các hàm số sau:
1, y= 2 - \(\sin\left(\dfrac{3\pi}{2}+x\right)\cos\left(\dfrac{\pi}{2}+x\right)\)
2, y= \(\sqrt{5-2\sin^2x.\cos^2x}\)
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
Tìm GTLN (max y), GTNN (min y) của y = x - 1 x 2 - x + 1 khi x ∈ - 1 ; 3
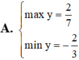

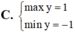
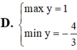
Tìm Max, Min của hàm số:
1) \(y=\dfrac{x+1+\sqrt{x-1}}{x+1+2\sqrt{x-1}}\)
2) \(y=\sin^{2016}x+\cos^{2016}x\)
3) \(y=2\cos x-\dfrac{4}{3}\cos^3x\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
4) \(y=\sin2x-\sqrt{2}x+1,x\in\left[0;\dfrac{\pi}{2}\right]\)
5) \(y=\dfrac{4-cos^2x}{\sqrt{sin^4x+1}},x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\)