Biết phương trình z 2 + a z + b = 0 ( a , b ∈ R ) có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Biết phương trình z 2 + a z + b = 0 với a, b thuộc R có một nghiệm z = 1- 2i. Tính a +b
A. 1
B. -5
C. -3
D. 3
Biết phương trình z 2 + a z + b = 0 với a, b thuộc R có một nghiệm z = 1+ 2i. Giá trị a + b bằng
A. 1
B. -5
C. -3
D. 3
Nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 là z = a + bi, a,b ∈ R. Tính a+ 3 b
A. 2
B. 1
C. –2
D. –1
Đáp án A
Phương pháp :
Tìm nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 bằng MTCT.
Cách giải:
Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là
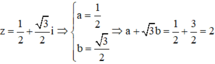
Biết phương trình z 2 + a z + b = 0 ( b , c ∈ R ) có một nghiệm z=1-i. Tính môđun của số phức w=a+bi.
![]()
![]()
![]()
![]()
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Đáp án D
Thay z=-2+i vào phương trình ta được:
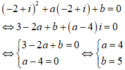
Vậy a-b=4-5=-1
Cách khác. Nghiệm liên hợp của nghiệm z 1 = - 2 + i là z 2 = - 2 - i
Ta có ![]() nên
z
1
,
z
2
là nghiệm của phương trình
nên
z
1
,
z
2
là nghiệm của phương trình ![]()
Do đó suy ra ![]()
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z=-2+i. Tính a+b
A. 9
B. 1
C. 4
D. -1
Đáp án A
Suy ra được nghiệm còn lại là
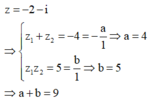
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z = -2 + i. Tính a + b
A. 9.
B. 1.
C. 4
D. -1
Cho a, b, c ε R, a # 0, z1 và z2 là hai nghiệm của phương trình az2 + bz + c = 0
Hãy tính z1 + z2 và z1 z2 theo các hệ số a, b, c.
Cho a, b, c ε R, a # 0, z1 và z2 là hai nghiệm của phương trình az2 + bz + c = 0
Hãy tính z1 + z2 và z1 z2 theo các hệ số a, b, c.
Áp dụng hệ thức Vi-et , ta có \(\begin{cases}z_1+z_2=-b\\z_1.z_2=c\end{cases}\)