Cho A, B là hai điểm thuộc hai nhánh khác nhau của đồ thị ( C ) : y = 2 x - 1 x - 1 . Lúc đó độ dài đoạn AB ngắn nhất bằng bao nhiêu?
![]()
![]()

![]()
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Gọi A, B là hai điểm thuộc hai nhánh khác nhau trên đồ thị (C) của hàm số y = x + 3 x − 3 , độ dài ngắn nhất của đoạn thẳng AB là
A. 2
B. 4
C. 3
D. 2 3
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0
A và B là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số y = x x - 2 . Khi đó độ dài đoạn AB ngắn nhất bằng
A. 4 2
B. 4
C. 2
D. 3
Gọi A,B là hai điểm thuộc hai nhánh khác nhau trên đồ thị (C) của hàm số 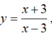 , độ dài ngắn nhất của đoạn thẳng AB là
, độ dài ngắn nhất của đoạn thẳng AB là
A.4 3 B.2 3 C. 2 3 D.4
B.2 3
C. 2 3
D.4
Đáp án A
Gọi A là điểm thuộc thuộc nhánh trái của đồ thị hàm số, nghĩa là
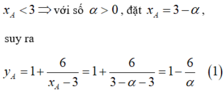
Tương tự gọi B là điểm thuộc nhánh phải, nghĩa là
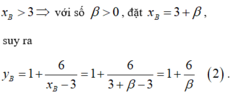
![]()
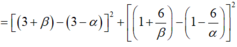
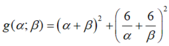
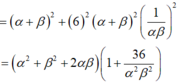
Biết A x A ; y B , B x B ; y B là 2 điểm thuộc hai nhánh khác nhau của đồ thị hàm số y = x + 1 x - 1 sao cho đoạn thẳng AB có đồ dài nhỏ nhất. Tính P = x A 2 + x B 2 + y A . y B
A. P = 5 + 2
B. P = 6 + 2
C. P = 6
D. P = 5
Biết A x A ; y A , B x B ; y B , là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số y = (x+1)/(x-1) sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính P = x A 2 + x B 2 + y A y B .
A. P = 6
B. P = 5 + 2
C. P = 6 + 2
D. P = 5
Gọi A, B là 2 điểm lần lượt thuộc 2 nhánh của đồ thị hàm số y = x + 1 x - 1 (C). Tìm khoảng cách ngắn nhất giữa hai điểm A, B
A. 16
B. 2 2
C. 2
D. 4
Tìm m để đường thẳng y= x+m (d) cắt đồ thị hàm số y= 2 x + 1 x - 2 (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị (C)
A. m ∈ R
B. m ∈ R \ { - 1 / 2 }
C. m > - 1 / 2
D. m < - 1 / 2