Cho cấp số nhân (un) biết u6 = 2 và u9 = 6. Giá trị của u21 bằng
A. 18.
B. 54.
C. 162.
D. 486.
Cho cấp số nhân (un) biết u6 = 2 và u9 = 6. Giá trị của u21 bằng
A. 18
B. 54
C. 162
D. 486
Chọn đáp án D
Gọi (un) có số hạng đầu u1 và công bội q.
Ta có u 6 = 2 u 9 = 6
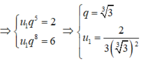
Suy ra u 21 = u 1 . q 20 = 2 3 ( 3 3 ) 2 . ( 3 3 ) 20 = 486
Cho cấp số nhân u n có số hạng đầu u 1 = 2 và số hạng thứ ba là u 3 = 18 . Giá trị của u 6 bằng
A. 486 hoặc - 486
B. 486
C. 972
D. 42
Đáp án A

Chú ý khi giải:
Nhiều HS sẽ chọn nhầm đáp án D vì đọc không kĩ đề thành cấp số “cộng”.
Nhiều em khác lại chọn nhầm B vì quên mất trường hợp q = -3
Cho cấp số nhân ( u n ) có số hạng đầu u 1 = 2 và số hạng thứ ba là u 3 = 18 . Giá trị của u 6 bằng
A. 486 hoặc -486
B. 486
C. 972
D. 42
Phương pháp:
- Tính công bội q, từ đó suy ra u 6
- Sử dụng công thức u n = u 1 q n - 1
Cách giải:
Ta có: u 3 = u 1 q 2 ⇔ q = ± 3
Vậy với q = 3 thì u 6 = u 1 . q 5 = 486
Với q = - 3 thì u 6 = u 1 . q 5 = - 486
Chọn: A
Cho cấp số nhân u n với công bội q Biết u 1 = 2 , u 6 = 486 . Tìm q
Ta có: u6 = u1.q5
hay 486 = 2.q5
⇒ q5 = 243
⇒ q = 3.
tìm un và q của cấp số nhân (un)
u6+u9=-7
2u4-u5=1
\(\left\{{}\begin{matrix}u_6+u_9=-7\\2u_4-u_5=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1.q^5+u_1.q^8=-7\\2u_1q^3-u_1q^4=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1q^3\left(q^2+q^5\right)=-7\\u_1q^3\left(2-q\right)=1\end{matrix}\right.\)
\(\Rightarrow q^5+q^2=-7\left(2-q\right)\)
\(\Rightarrow\left(q+2\right)\left(q^4-2q^3+4q^2-7q+7\right)=0\)
\(\Rightarrow q=-2\)
\(\Rightarrow u_1=-\dfrac{1}{32}\)
Cho cấp số nhân (un) có u2=6 và u5=48. Biết tổng n số hạng đầu tiên của cấp số nhân đã cho bằng 381. Giá trị của n nằm trong khoảng nào? A. (3;5) B. (10;12) C. (6;11) D. (11;20)
Đáp án là C. Vì:
Gọi d là công bội của dãy cấp số nhân \((u_n) \)
⇒ \(u_n=d.u_{n-1}=d^2.u_{n-2}=...=d^{n-2}.u_2=d^{n-1}.u_1\)
Suy ra: \(u_5=d^3.u_2 \Rightarrow d^3=\dfrac{u_5}{u_2}=\dfrac{48}{6}=8 \Rightarrow d=2\)
Có: \(u_2=d.u_1 \Leftrightarrow u_1=\dfrac{u_2}{d}=\dfrac{6}{2}=3\)
Theo đề: \(u_1+u_2+...+u_n=381 \)
\(\Leftrightarrow u_1+d.u_1+d^2.u_1+...+d^{n-1}u_1=381\)
\(\Leftrightarrow u_1(1+d+d^2+...+d^{n-1})=381\)
Mặt khác: \(u_1(1+d+d^2+...+d^{n-1})=3.\dfrac{d^n-1}{d-1} =3.\dfrac{2^n-1}{2-1}=3.(2^n-1)\)
\(\Rightarrow 3.(2^n-1)=381 \Leftrightarrow 2^n-1=127 \Leftrightarrow 2^n=128=2^7 \Rightarrow n=7\).
Vậy n = 7 thuộc (6;11)
Cho cấp số nhân u n có số hạng đầu u 1 = 2 và u 4 = 54 Giá trị u 2019 bằng
A. 2 . 3 2020
B. 2 . 2 2020
C. 2 . 3 2018
D. 2 . 2 2018
1/2 + 1/6 + 1/18 + 1/54 + 1/162 + 1/486 + 1/1458
Giá trị của biểu thứ trên là một phân số tối giản
Cho cấp số cộng ( u n ) có công sai d , u 6 = 6 và u 12 = 18 thì
A. u 1 = 4 , d = − 2
B. u 1 = 4 , d = 2
C. u 1 = − 4 , d = 2
D. u 1 = − 4 , d = − 2
Đáp án C
u 12 = 18 = u 1 + 11 d u 6 = 6 = u 1 + 5 d ⇔ u 1 = − 4 d = 2