Nếu ∫ 1 2 1 ( x - 3 ) ( x - 4 ) d x = ln ( m ) thì m bằng:
![]()
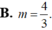
![]()
![]()
Tìm x nếu (x^2-4x+1)^3=(x^2-x-1)^3-(3x-2)^3
Vẽ đồ thị hàm số sau
1 , \(y=\left\{{}\begin{matrix}3x\\x\end{matrix}\right.\) nếu x\(\ge\) 0 , nếu x<0
2 , y = \(\left\{{}\begin{matrix}3x-2\\-3x+2\end{matrix}\right.\)nếu \(x\ge\frac{2}{3}\) , nếu x<\(\frac{2}{3}\)
3 y = \(\left\{{}\begin{matrix}2x-1\\\frac{1}{2}x+1\end{matrix}\right.\) nếu x\(\ge\)1 , nếu x<1
Những câu sau đúng hay sai, nếu sai hãy sửa lại cho đúng
1, (a-b). (a+b) = (a+b)^2
=( nếu sai sửa tại đây)
2, (x-3).(x+3) = x^2 -9
=
3,x^2 - 2x +1 =(x-1)^2
=
4,(x-3)^2 =( 3-x) ^2
=
5,(x-3)^3 =(3-x)^3
=
Giúp mình với ạ mình cần gấp
1 sai
(a-b).(a+b)=a^2-b^2
2 đúng
3 đúng
4 sai
(x-3)^2=-(3-x)^2
5 sai
(x-3)^3=-(3-x)^3
Câu 29. Nếu 1/3 : (1/6 - 1/2) <_ x <_ 2/3 x (-1/6 + 3/4) thì giá trị của x bằng :
A.0
B.1
C.2
D.3
\(\dfrac{1}{3}:\left(\dfrac{1}{6}-\dfrac{1}{2}\right)< =x< =\dfrac{2}{3}\left(-\dfrac{1}{6}+\dfrac{3}{4}\right)\)
=>\(\dfrac{1}{3}:\left(\dfrac{1}{6}-\dfrac{3}{6}\right)< =x< =\dfrac{2}{3}\left(-\dfrac{2}{12}+\dfrac{9}{12}\right)\)
=>\(\dfrac{1}{3}:\dfrac{-2}{6}< =x< =\dfrac{2}{3}\cdot\dfrac{7}{12}\)
=>\(\dfrac{1}{3}\cdot\dfrac{-6}{2}< =x< =\dfrac{14}{24}=\dfrac{7}{12}\)
=>\(-1< =x< =\dfrac{7}{12}\)
=>Chọn A
Câu 29. Nếu 1/3 : (1/6 - 1/2) <_ x <_ 2/3 x (-1/6 + 3/4) thì giá trị của x bằng :
A.0
B.1
C.2
D.3
Nếu (x^2-1/3)(x^4+x^2/3+1/9)=x^6-a thì a=...
Bài 1: cho 2(x-3)=3(y+2);3(2-z)=3(y+2) và 2x-3y+z=-4
tính x-y+z
Bài 2:Cho x tỉ lệ nghịch với y Nếu y1=2;y2=8 và 3x1+6x2=(1/13)^-1. Tìm y nếu x=-12
nếu 1-1/2 x 1-1/3 x .....x 1- 1/2014 x1 -1/2015 x a =1 thì a
là lấy cái này cộng cái này rồi nhân cái này sẽ ra kết quả
chứng minh : 3^(x+3)+3^(x+1)+2^(x+3)+2^(x+2) chia hết cho 6
giải thích : nếu x=1 thì 3^(x+3)=3^4
\(3^{x+1}\)\(+3^{x+3}+2^{x+3}+2^{x+2}\)
= \(3^x.3+3^x.9+2^x.8+2^x.4\)
=\(3^x.12+2^x.12\)
=\(12\left(3^x+2^x\right)\)
vì 12 chia hét cho 6=> bt trên cx chia hét cho 6
Tìm Min(Max) nếu có thể
E=-x^2+2*x-1;
C=(x^2-1)*(3*x-10)*(3*x-16)
mik đag cần gấp
E = - \(x^2\) + 2\(x\) - 1
E = - (\(x^2\) - 2\(x\) + 1)
E = - (\(x\) - 1)2
(\(x\) - 1) ≥ 0 ⇒ - (\(x\) - 1)2 ≤ 0
Emax = 0 ⇔ \(x\) = 1
Để tìm các điểm tới hạn của hàm E, chúng ta cần tìm các giá trị của x tại đó đạo hàm của E bằng 0.
Lấy đạo hàm của E theo x, ta được:
E' = -2x + 2
Đặt E' bằng 0 và tìm x:
-2x + 2 = 0
-2x = -2
x = 1
Vậy điểm tới hạn của E là x=1.
Để tìm các điểm tới hạn của hàm C, chúng ta cần tìm các giá trị của x tại đó đạo hàm của C bằng 0.
Lấy đạo hàm của C theo x, ta được:
C' = (2x)(3x-10)(3x-16) + (x^2-1)(3)(3x-10) + (x^2-1)(3)(3x-16)
Đặt C' bằng 0 và giải tìm x:
(2x)(3x-10)(3x-16) + (x^2-1)(3)(3x-10) + (x^2-1)(3)(3x-16) = 0
Phương trình này khá phức tạp và không có nghiệm đơn giản. Nó sẽ yêu cầu thao tác đại số hơn nữa hoặc các phương pháp số để tìm các điểm tới hạn của C.
\(...E=x^2+2x+1-2\)
\(\Rightarrow E=\left(x+1\right)^2-2\ge-2\)
(Vì \(\left(x+1\right)^2\ge0,\forall x\))
Suy ra Min(E)=-2