Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:x-y-3=0 và điểm A(2;6). Trên đường thẳng d lấy hai điểm B và C sao cho tam giác ABC vuông tại A và có diện tích bằng 35 2 2 . Phương trình đường tròn ngoại tiếp tam giác ABC là:
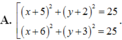
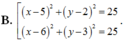
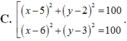
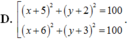
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 2x+y-2z-2 = 0 và đường thẳng có phương trình d : x + a 1 = y + 2 2 = z + 3 2 và điểm A(1/2;1;1) Gọi ∆ là đường thẳng nằm trong mặt phẳng (α) , song song với d, đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/3
B. 7/2
C. 21 2
D. 3/2
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x - 2 y - 3 = 0 . Tọa độ hình chiếu vuông góc H của điểm M (0;1) trên đường thẳng là
A. H (-1;2)
B. H (5;1)
C. H (3;0)
D. H (1; -1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : 2 x + y − 2 z − 2 = 0 và đường thẳng có phương trình d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d, đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7 3 .
B. 7 2 .
C. 21 2 .
D. 3 2 .
Đáp án B.
Dễ thấy d ⊥ α và − 1 ; − 2 ; − 3 ∈ α ⇒ d ⊂ α .
Ta có B = Δ ∩ Oxy ⇒ B a ; b ; 0 mà B ∈ Δ ⊂ α ⇒ 2 a + b − 2 = 0 (1).
Lại có d / / Δ ⇒ d d ; Δ = d B ; d = 3.
Đường thẳng d đi qua M 0 ; 0 ; − 1 , có u d → = 1 ; 2 ; 2 .
Do đó:
d B ; d = B M → ; u d → u d → = 2 b − 2 2 + 1 − 2 a 2 + 2 a − b 2 3 = 3 2
Từ (1), (2) suy ra:
a ; b = − 1 ; 4 → B − 1 ; 4 ; 0 a ; b = 2 ; − 2 → B 2 ; − 2 ; 0 .
Vậy A B = 7 2 .
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-1), đường thẳng d : x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P): x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Đáp án C
HD: Gọi H(1+2t;-1+t;2-t) là hình chiếu của A trên d
![]()
![]()
Suy ra H(3;0;1), phương trình đường thẳng AH là
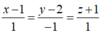
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, điểm C có hòanh độ dương và nằm trên đường thẳng \(d:x-y+1=0\) , có điểm A ( 2;-1). Viết pt đường thẳng BD, biết rằ BD \(=\sqrt{26}\) và BD tạo với chiều dương trục hoành một góc nhọn
( Help me !!!)
Trong mặt phẳng tọa độ Oxy, tìm điểm A thuộc trục hoành và điểm B thuộc trục tung sao cho A và B đối xứng với nhau qua đường thẳng \(d:x-2y+3=0\)
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A ( 1 2 ; 1 ; 1 ) . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/2
B. 21 / 2
C. 7/3
D. 3/2
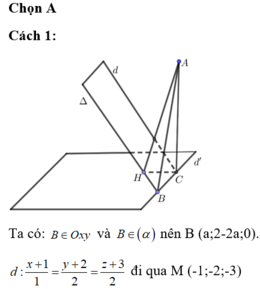
Ta có: d ⊂ (α) nên d và ∆ song song với nhau và cùng nằm trong mặt phẳng (α).
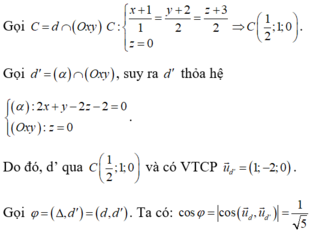


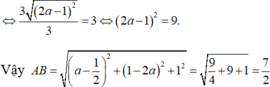
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; − 1 , đường thẳng d : x − 1 2 = y + 1 1 = z − 2 − 1 và mặt phẳng P : x + y + 2 z + 1 = 0 . Điểm B thuộc mặt phẳng P thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. 3 ; − 2 ; − 1
B. − 3 ; 8 ; − 3
C. 0 ; 3 ; − 2
D. 6 ; − 7 ; 0