△ A B C cân tại A, AB = a, A B C ^ = 120 o . Cho △ A B C quay quanh BA tạo thành một khối tròn xoay có thể tích V. Tính V
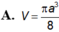
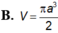
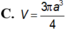
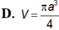
Cho AABC cân tại A. Vẽ trung tuyến AM . Kẻ MK song song với AB (K thuộc AB) a) Chứng minh AABM= AACM. b) Cm: AAKM cân c) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với ÁC tại C, hai đường này cắt nhau tại D. Chứng minh A, M, D thẳng hàng.
a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
=>ΔAMB=ΔAMC
b: Xét ΔABC có
M là trung điểm của CB
MK//AB
=>K là trung điểm của AC
ΔAMC vuông tại M
mà MK là trung tuyến
nên MK=AK
=>ΔKAM cân tại K
c: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>DB=DC
=>D nằm trên trung trực của BC(1)
ΔABC cân tại A
mà AM là trung tuyến
nên AM là trung trực của BC(2)
Từ (1), (2) suy ra A,M,D thẳng hàng
Cho AABC cân tại A. Vẽ trung tuyến AM . Kẻ MK song song với AB (K thuộc AB) a) Chứng minh AABM= AACM. b) Cm: AAKM cân c) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với ÁC tại C, hai đường này cắt nhau tại D. Chứng minh A, M, D thẳng hàng.
a, Xét tam giác ABM va Tam giác ACM :
có MB=MC (AM là trung tuyên của tam giác cân ABC)
Có AM chung
AC=AB (Tam giác ABC là tam giác cân tại A)
=>Tam giác ABM= Tam giác ACM
b:
có MK//AB => góc KMC= góc ABC (2 góc đồng vị)
mà góc ACB=góc ABC (2 góc dáy của tam giác ABC cân tại A)
=>góc KMC= góc KCM (cùng bằng góc ABC)
có AM là trung tuyến của tam giác cân ABC tại A => Am đồng thười là đg cao=> AM vuông góc vs BC tại M=> góc AMK+góc KMC =90 dộ
Có AM là đk cao của tam giác ABC tại M (CMT)
=> MAC+ MCA= 90 độ (có AM là đk cao); AMK+KMC=90 độ
mà góc KCM= góc KMC (CMT)
===> góc KAM= góc KMA (cùng phụ vs góc KMC 1 góc 90 dộ)
===> Tam giác KAM cân tại K ( điều phải chúng minh)
c;
Có AB vuông góc vs BD tại B =>góc ABD= 90*
Tương tự có Góc ACD=90*
mà góc ABC= góc ACB (CMT)
=> góc CBD= góc BCD
==> Tam giác BCD cân tại D
mà M là trung điểm của BC (giả thiết)
=> md cũng là đk cao của Tam giác cân BCD
=> góc ADM thằng hàng (định ly: có duy nhất 1 đg thằng đi qua 1 điểm và vuông góc vs đg thẳng tại điểm đó)
Cho tam giác ABC vuông tại A, tại C kẻ đường phân giác cắt BC tại D. Từ D kẻ DE vuông góc BC a)c/m tam giác ACD=tam giác ACE b)c/m tam giác ADE cân c)cho AB=12 cm, AC=13. Tính BC, tính chu vi tam giác ABC
Sửa đề: cắt AB tại D.
a) Sửa đề: ΔACD=ΔECD
Xét ΔACD vuông tại A và ΔECD vuông tại E có
CD chung
\(\widehat{ACD}=\widehat{ECD}\)(CD là tia phân giác của \(\widehat{ACE}\))
Do đó: ΔACD=ΔECD(Cạnh huyền-góc nhọn)
b) Ta có: ΔACD=ΔECD(cmt)
nên DA=DE(Hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)
Cho tam giác ABC cân (AB = AC). Các đường trung trực của AB và AC cắt nhau tại O và cắt BC tại M và N (M và N nằm ngoài đoạn thẳng BC). Chứng minh:
a) ∆ A M B và ∆ A N C cân;
b) ∆ A M C = ∆ N B ;
c) AO là đường trung trực của MN.
cho hình thang abcd (ab//cd,ab<cd).hai tia phan giác củ hai góc c và d cắt nhau tại k thuộc đáy ab . chứng minh : a, tam giác adk cân tại a, tam giác bkc cân tại b. b,ad bc=ab
a) Ta có: \(\widehat{AKD}=\widehat{KDC}\)(hai góc so le trong, AK//CD)
mà \(\widehat{ADK}=\widehat{KDC}\)(DK là tia phân giác của \(\widehat{ADC}\))
nên \(\widehat{AKD}=\widehat{ADK}\)
hay ΔAKD cân tại A
Ta có: \(\widehat{BKC}=\widehat{KCD}\)(hai góc so le trong, BK//CD)
mà \(\widehat{KCD}=\widehat{BCK}\)(CK là tia phân giác của \(\widehat{BCD}\))
nên \(\widehat{BKC}=\widehat{BCK}\)
hay ΔBKC cân tại B
Tam giác ABC cân tại A,AB=AC. Tia phân giác góc B và C cắt AC và Ab lần lượt tại D và E. Chứng Minh:
a, Tam giác AED cân đỉnh A.
b,DE song song BC
c,BE=ED=DC
a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
Tam giác ABC cân tại A,AB=AC. Tia phân giác góc B và C cắt AC và AB lần lượt tại D và E. Chứng Minh:
a, Tam giác AED cân đỉnh A.
b,DE song song BC
c,BE=ED=DC
a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
tham khảo á
làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50
Cho tam giác ABC cân tại A có AB = AC = 10 cm;BC = 12 cm.Kẻ AH vuông góc với BC. a) Chứng minh HB = HC;tính AH. b) kẻ Bx vuông góc với AB tại B; Cy vuông góc với AC tại C; Bx và Cy cắt nhau tại M. chứng minh AM là tia phân giác của góc BAC và suy ra A,H,M thẳng hàng. c)kẻ HK song song với MB(K thuộc MC) Trên tia HM lấy điểm O sao cho OM = 2OH. Chứng minh ba điểm B,O,K thẳng hàng
Câu c. lên lớp 8 thì em có thể dùng đường trung bình dễ hơn nhiều nhé.

Tam giác ABC cân tại A,AB=AC. Tia phân giác góc B và C cắt AC và AB lần lượt tại D và E. Chứng Minh:
a, Tam giác AED cân đỉnh A.
b,DE song song BC
c,BE=ED=DC
a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
EBC = DCB (cmt)
BC là cạnh chung
ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180o - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180o - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
c) bớt ED đi, c/m ở trên r`
a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
EBC = DCB (cmt)
BC là cạnh chung
ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180o - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180o - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
c) bớt ED đi, c/m ở trên r`
| Bài 3 : Cho AABC cân tại A , kẻ AH vuông góc với BC ( HEBC ) . Biết AB = 15 cm ; AH = 12 cm . a ) Tính độ dài BH ? b ) Chứng minh HB = HC . c ) Kẻ HM vuông góc với AB , kẻ HN vuông góc với AC . Chứng minh : HM = HN . d ) Qua B , kẻ đường thẳng vuông với BC cắt tia CA tại D . Chứng minh rằng AABD cân .