Tìm m để phương trình sin2x+ cos2x= m/2 có nghiệm
![]()
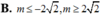
![]()
![]()
Tìm tất cả giá trị của m để phương trình sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m có nghiệm?
A. 0 ≤ m ≤ 1
B.m> 1
C.0< m< 1
D. m ≤ 0
Hướng dẫn giải:
Chọn A.
Ta có: sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m
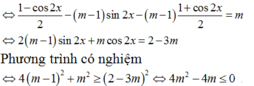
![]()
Tìm m để phương trình sau có nghiệm:
\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt{3}.sin2x-cos2x\)
\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt[]{3}sin2x-cos2x\)
\(\Leftrightarrow4.\left(-\dfrac{1}{2}\right)\left[sin\left(x+\dfrac{\pi}{3}+x-\dfrac{\pi}{6}\right)+sin\left(x+\dfrac{\pi}{3}-x+\dfrac{\pi}{6}\right)\right]=m^2+2.\left[\dfrac{\sqrt[]{3}}{2}.sin2x-\dfrac{1}{2}.cos2x\right]\)
\(\Leftrightarrow2\left[sin\left(2x+\dfrac{\pi}{6}\right)+sin\left(2x-\dfrac{\pi}{6}\right)\right]=m^2+2\)
\(\Leftrightarrow2.2sin2x.cos\dfrac{\pi}{6}=m^2+2\)
\(\Leftrightarrow2.2sin2x.\dfrac{\sqrt[]{3}}{2}=m^2+2\)
\(\Leftrightarrow2\sqrt[]{3}sin2x.=m^2+2\)
\(\Leftrightarrow sin2x.=\dfrac{m^2+2}{2\sqrt[]{3}}\)
Phương trình có nghiệm khi và chỉ khi
\(\left|\dfrac{m^2+2}{2\sqrt[]{3}}\right|\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m^2+2}{2\sqrt[]{3}}\ge-1\\\dfrac{m^2+2}{2\sqrt[]{3}}\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge-2\left(1+\sqrt[]{3}\right)\left(luôn.đúng\right)\\m^2\le2\left(1-\sqrt[]{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow-\sqrt[]{2\left(1-\sqrt[]{3}\right)}\le m\le\sqrt[]{2\left(1-\sqrt[]{3}\right)}\)
Có bao nhiêu số nguyên m để phương trình sin x - cos x - 2 cos 2 x + m =m+sin2x+cos2x có nghiệm thực.
A. 3.
B. 9.
C. 2.
D. 5.
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Số giá trị nguyên của tham số m thuộc đoạn − 2018 ; 2018 để phương trình m + 1 sin 2 x − sin 2 x + c os 2 x = 0 có nghiệm là:
A. 4037
B. 4036
C. 2019
D. 2020
Đáp án D
P T ⇔ m + 1 1 − c os 2 x 2 − sin 2 x + cos 2 x = 0 ⇔ sin 2 x + m − 1 2 c os 2 x = m + 1 2 .
PT có nghiệm ⇔ 1 2 + m − 1 2 2 ≥ m + 1 2 2 ⇔ m ≤ 1.
Vì m ∈ − 2018 ; 2018 ⇒ có 2020 giá trị nguyên của m.
1. Các nghiệm của phương trình \(\sqrt{3}sin2x-cos2x-2=0\) là?
2. Hàm số \(y=2cos3x+3sin3x-2\) có tất cả bao nhiêu giá trị nguyên dương?
3. Tìm tham số m để phương trình \(msinx-cosx=\sqrt{5}\) có nghiệm
Giúp mk với ạ!
1, Phương trình tương đương
\(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
⇔ \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
⇔ \(2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k.2\pi\)
⇔ x = \(\dfrac{\pi}{3}+k.\pi\)
2, \(2cos3x+3sin3x-2\)
= \(\sqrt{13}\)\((\dfrac{2}{\sqrt{13}}cos3x+\dfrac{3}{\sqrt{13}}sin3x)\) - 2
Do \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{3}{\sqrt{13}}\right)^2=1\) nên tồn tại 1 góc a sao cho \(\left\{{}\begin{matrix}sina=\dfrac{2}{\sqrt{13}}\\cosa=\dfrac{2}{\sqrt{13}}\end{matrix}\right.\)
BT = \(\sqrt{13}sin\left(x+a\right)-2\)
Do - 1 ≤ sin (x + a) ≤ 1 với mọi x và a
⇒ \(-\sqrt{13}-2\le BT\le\sqrt{13}-2\)
⇒ \(-5,6< BT< 1,6\)
Vậy BT nhận 5 giá trị nguyên trong tập hợp S = {-5 ; -4 ; -3 ; -2 ; -1}
3. \(msinx-cosx=\sqrt{5}\)
⇔ \(\dfrac{m}{\sqrt{m^2+1}}.sinx-\dfrac{1}{\sqrt{m^2+1}}.cosx=\dfrac{\sqrt{5}}{\sqrt{m^2+1}}\)
⇔ sin(x - a) = \(\sqrt{\dfrac{5}{m^2+1}}\) với \(\left\{{}\begin{matrix}sina=\dfrac{1}{\sqrt{m^2+1}}\\cosa=\dfrac{m}{\sqrt{m^2+1}}\end{matrix}\right.\)
Điều kiện có nghiệm : \(\left|\sqrt{\dfrac{5}{m^2+1}}\right|\le1\)
⇔ m2 + 1 ≥ 5
⇔ m2 - 4 ≥ 0
⇔ \(\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Tìm m để các bất phương trình 4 sin 2 x + cos 2 x + 17 3 cos 2 x + sin 2 x + m + 1 ≥ 2 đúng với mọi x ∈ R.
A. 10 - 3 < m ≤ 15 - 29 2
B. 10 - 1 < m ≤ 15 - 29 2
C. 10 - 1 < m ≤ 15 + 29 2
D. 10 - 1 < m < 10 + 1
2cos2x-sin2x-sin2x=m+1 tìm m để phương trình có nghiệm \(\dfrac{\pi}{2}\)+kπ
(m^2 +m)cos2x =m^2 -m -3 -m^2cos2x. Tìm m để phương trình có nghiệm
`(m^2+m)cos2x=m^2-m-3-m^2 cos2x`
`<=> (2m^2+m)cos2x=m^2-m-3`
`<=>cos2x =(m^2-m-3)/(2m^2+m)`
PT có nghiệm `<=> -1 <= (m^2-m-3)/(2m^2+m) <=1`
`<=> [(m<=-1 \vee m>=1),(-1/2 < m <0):}`