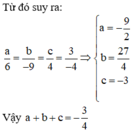Mặt cầu đi qua A(4; -5; 5) và tiếp xúc các mặt phẳng tọa độ có bán kính lớn nhất (Rmax) là:
![]()
![]()
![]()
![]()
Khẳng đỉnh nào sau đây là sai?
A. Có một mặt cầu đi qua các đỉnh của một tứ diện bất kì.
B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.
C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.
D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.
Chọn B.
Nếu có một mặt cầu ngoại tiếp lăng trụ thì đáy của lăng trụ phải nội tiếp trong một đường tròn, điều này không đúng cho tứ giác lồi bất kì.
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
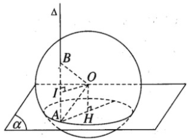
Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có OI ⊥ AB. Vì AB // OH nên AIOH là hình chữ nhật.
Do đó
![]()
Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc ∠ OAB = 60 ° nên OAB là tam giác đều và suy ra AB = OA = OB = r.
Mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với 3 mặt phẳng ![]() .Bán kính mặt cầu (S) là
.Bán kính mặt cầu (S) là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
![]()
![]()
![]()
![]()
Lập phương trình mặt cầu (S), biết S đi qua C (2; -4; 3) và đi qua các hình chiếu của C lên
a) 3 trục toạ độ
b) 3 mặt phẳng toạ độ
Gọi I(a;b;c) và r lần lượt là tâm và bán kính mặt cầu (S).
Phương trình mặt cầu (S) có dạng: (x-a)2+(y-b)2+(z-c)2=r2.
a) (S) đi qua các điểm C(2;-4;3), (2;0;0), (0;-4;0) và (0;0;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+c^2=r^2\\a^2+\left(-4-b\right)^2+c^2=r^2\\a^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.
b) (S) đi qua các điểm C(2;-4;3), (2;-4;0), (2;0;3) và (0;-4;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+\left(-4-b\right)^2+c^2=r^2\\a^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.
Gọi (S) là mặt cầu đi qua 4 điểm A(2;0;0),B(1;3;0),C(-1;0;3),D(1;2;3) . Tính bán kính R của (S).
A. R = 2 2
B. R = 6
C. R = 3
D. R = 6
Chọn B.
Phương pháp:
- Gọi I (a;b;c) là tâm mặt cầu.
- Lập hệ phương trình ẩn a,b,c dựa vào điều kiện IA = IB = IC = ID .
Cách giải:
Gọi I (a;b;c) là tâm mặt cầu đi qua bốn điểm A(2;0;0) ,B(1;3;0) ,C(-1;0;3) ,D(1;2;3) .
Khi đó
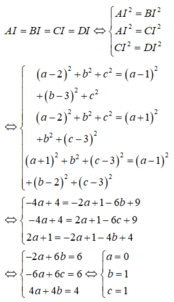
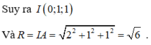
Gọi (S) là mặt cầu đi qua 4 điểm A(2;0;0),B(1;3;0),C(-1;0;3),D(1;2;3) . Tính bán kính R của (S)
![]()
![]()
![]()
![]()
Chọn B
Phương pháp:
- Gọi I (a;b;c) là tâm mặt cầu.
- Lập hệ phương trình ẩn a,b,c
dựa vào điều kiện IA = IB = IC = ID .
Cách giải:
Gọi I (a;b;c) là tâm mặt cầu đi qua bốn điểm A(2;0;0) ,B(1;3;0) ,C(-1;0;3) ,D(1;2;3) .
<=>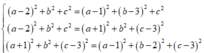
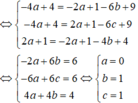
Suy ra I(0;1;1) và ![]()
Trong không gian Oxyz hãy viết phương trình mặt cầu đi qua bốn điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; 4) và gốc tọa độ O. Hãy xác định tâm và bán kính của mặt cầu đó.
Phương trình mặt cầu (S) cần tìm có dạng: x 2 + y 2 + z 2 – 2ax – 2by – 2cz + d = 0.
Vì
A ∈ (S) nên ta có: 1 – 2a + d =0 (1)
B ∈ (S) nên ta có: 4 + 4b + d = 0 (2)
C ∈ (S) nên ta có: 16 – 8c + d = 0 (3)
D ∈ (S) nên ta có: d = 0 (4)
Giải hệ 4 phương trình trên ta có: d = 0, a = 1/2, b = −1,c = 2.
Vậy mặt cầu (S) cần tìm có phương trình là: x 2 + y 2 + z 2 –x + 2y – 4z = 0
Phương trình mặt cầu (S) có thể viết dưới dạng:
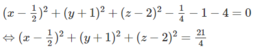
Vậy mặt cầu (S) có tâm I(1/2; -1; 2) và có bán kính 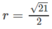
Trong không gian Oxyz, cho hai điểm A (1;2;4), B (0;0;1) và mặt cầu S : x + 1 2 + y - 1 2 + z 2 = 4 . Mặt phẳng P : a x + b y + c z + 3 = 0 đi qua A, B và cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính T = a + b + c
A. T = - 3 4
B. T = 33 5
C. T = 27 4
D. T = 31 5
Chọn A.
Phương pháp:
Cách giải: Tâm mặt cầu là I(-1;1;0) bán kính mặt cầu là R = 2.