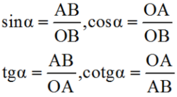Cho góc nhọn α
Chứng minh rằng: 1 - t g α 1 + t g α = cos α - sin α cos α + sin α
Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng S A B C D = 1/2.AC.BD.sin α .
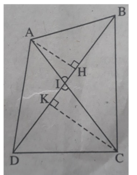
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠ (AIB) = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin α , CK = CI.sin α
Diện tích tam giác ABD là S A B D = 1/2 BD.AH.
Diện tích tam giác CBD là S C B D = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = S A B D + S C B D = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin α = 1/2BD.AC.sin α
Cho α là góc nhọn, chứng minh rằng:
1 - tan α 1 + tan α = cos α - sin α cos α + sin α
Cho các góc α, β nhọn. Chứng minh rằng cos(α + β ) = cosαcosβ - sinαsinβ .
cho góc nhọn α :
chứng minh rằng: \(\frac{1-\tan\text{α}}{1+\tan\text{α}}\)=\(\frac{\cos\text{α}-\sin\text{α}}{\cos\text{α}+\sin\text{α}}\)
\(\frac{1-tana}{1+tana}=\frac{1-\frac{sina}{cosa}}{1+\frac{sina}{cosa}}=\frac{\frac{1}{cosa}\left(cosa-sina\right)}{\frac{1}{cosa}\left(cosa+sina\right)}=\frac{cosa-sina}{cosa+sina}\)
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
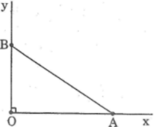
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có: sin 2 α + cos 2 α = 1
Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
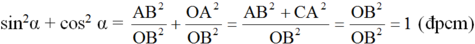
cho góc nhọn α tuỳ chọn chứng minh rằng
a) 1+\(\tan^2\) α=1\(\dfrac{1}{\cos^2}\) α
VT `=1+tan^2 α`
`=1+ (sin^2α)/(cos^2α)`
`= (cos^2α+sin^2α)/(cos^2α)`
`= 1/(cos^2α)`
a, \(1+tan^2a=\dfrac{1}{\cos^2a}\)
ĐT \(\Leftrightarrow\cos^2a\left(1+\tan^2a\right)=1\)
\(\Leftrightarrow\cos^2a+\cos^2a.\tan^2a=1\)
\(\Leftrightarrow\cos^2a.\dfrac{\sin^2a}{\cos^2a}+\cos^2a=\sin^2a+\cos^2a=1\) ( ĐT đã có )
=> ĐPCM
Vậy ...
Dựng góc nhọn α , biết rằng: cos α = 0,75 tg α = 1
*Cách dựng:
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
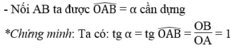
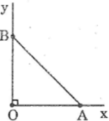
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
t g α = sin α cos α , c o t α = cos α sin α , t a α . c o t g α = 1
Gợi ý: Sử dụng định lí Pitago.
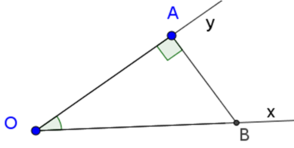
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: