Phương trình của đường thẳng AB có dạng: y = ax + b.

Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:

5 = a.4 + b (1)

-1 = a.1 + b (2)

Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.

Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.

Vậy phương trình đường thẳng AB là: y = 2x – 3.

Làm tương tự như trên, ta có:

Phương trình đường thẳng BC là: y = -x.

Phương trình đường thẳng CD là: y = x – 8.

Phương trình đường thẳng DA là: y = -2x + 13.

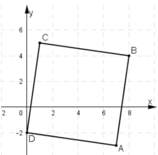
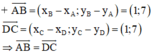
⇒ ABCD là hình bình hành.

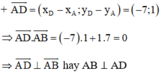
⇒ hình bình hành ABCD là hình chữ nhật.

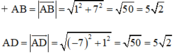
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).

* Gọi phương trình đường thẳng AB là y = ax + b.

Tọa độ các điểm A, B phải thỏa mãn phương trình y = ax + b nên ta có:

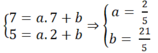
Vậy phương trình của đường thẳng AB là y = 2/5x + 21/5.

*Gọi phương trình của đường thẳng BC là y = a’x + b’.

Tương tự như trên ta có:

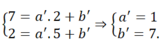
Vậy phương trình của đường thẳng BC là y = -x + 7.

*Gọi phương trình của đường thẳng AC là y = a’’x + b’’.

Tương tự như trên ta có: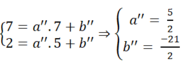 

Vậy phương trình của đường thẳng AC là y = 5/2x - 21/2.

a: Khi x=0 thì y=4

Khi y=0 thì -2x+4=0

hay x=2

b: Gọi điểm cần tìm là A(x;x)

Thay y=x vào y=-2x+4, ta được:

x=-2x+4

=>x=4

Vậy: Điểm cần tìm là A(4;4)

\(\overrightarrow{AB}=\left(-3;7\right)\)

\(\overrightarrow{DC}=\left(1-x_D;5-y_D\right)\)

Để ABCD là hbh thì 

\(\left\{{}\begin{matrix}1-x_D=-3\\5-y_D=7\end{matrix}\right.\Leftrightarrow D\left(2;-2\right)\)

Ta có

A B → = 1 ; 7 ⇒ A B = 1 2 + 7 2 = 5 2 B C → = − 7 ; 1 ⇒ B C = 5 2 C D → = − 1 ; − 7 ⇒ C D = 5 2 D A → = 7 ; − 1 ⇒ D A = 5 2 ⇒ A B = B C = C D = D A = 5 2 .

Lại có:  A B → . B C → = 1 − 7 + 7.1 = 0  nên A B ⊥ B C .

Từ đó suy ra ABCD là hình vuông.

Chọn C.

Chọn C

a: A(2;4); B(1;0); C(2;2)

vecto AB=(-1;-4)

vecto DC=(2-x;2-y)

Vì ABCD là hình bình hành nên vecto AB=vecto DC

=>2-x=-1 và 2-y=-4

=>x=3 và y=6

c: N đối xứng B qua C

=>x+1=4 và y+0=4

=>x=3 và y=4

a: A(2;4); B(1;0); C(2;2)

vecto AB=(-1;-4)

vecto DC=(2-x;2-y)

Vì ABCD là hình bình hành nên vecto AB=vecto DC

đây nhé bạn

=>2-x=-1 và 2-y=-4

=>x=3 và y=6

c: N đối xứng B qua C

=>x+1=4 và y+0=4

=>x=3 và y=4

Lời giải

Tổng quát

trong mặt phẳng tọa Oxy Đường thẳng có phương trình

y=a x +b

.........Vấn đề ta phải đi xác định các hệ số : a,b

a)

a.1) đi qua A;B

a,b thủa mãn hệ phương trình

\(\left\{{}\begin{matrix}4a+b=5\\a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=-3\end{matrix}\right.\) \(\Rightarrow\left(AB\right)d_1:y=2x-3\)

a.2) đi Qua BC

a,b thủa mãn hệ phương trình

\(\left\{{}\begin{matrix}4a+b=-4\\a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow\left(BC\right)d_2:y=-x\)

a.3) đi qua CD

a,b thủa mãn hệ phương trình

\(\left\{{}\begin{matrix}4a+b=-4\\7a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-8\end{matrix}\right.\) \(\Rightarrow\left(CD\right)d_3:y=x-8\)

a.4) đi qua DA

a,b thủa mãn hệ phương trình

\(\left\{{}\begin{matrix}4a+b=5\\7a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=13\end{matrix}\right.\)\(\Rightarrow\left(DA\right)d_4:y=-2x-13\)

việc sử dụng máy tính ==> suy ra ra góc --> cái đó quá tầm thường rồi.

Mấu chốt vấn Vấn đề biết ý nghĩa hệ số "a" => ra tất cả

ý nghĩa hệ số a vẫn có vị rất quan trọng trong tọa độ phẳng (tương đương sức f(1) trong phương trình đại số )

nhiều bài toán biết cách vận dụng nó -->bài toán trở lên quá đơn giải --> dẫn đến bất ngờ