Có thể giúp em trước 17h đc ko ạ🥲
H24
Những câu hỏi liên quan
bài này em ko hiểu có thể giải giúp em đc ko ạ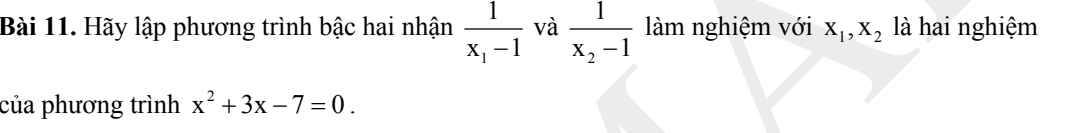
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Đúng 1
Bình luận (0)
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Đúng 0
Bình luận (0)
Có thể giải giúp em đc ko ạ chiều em thi rồi ạ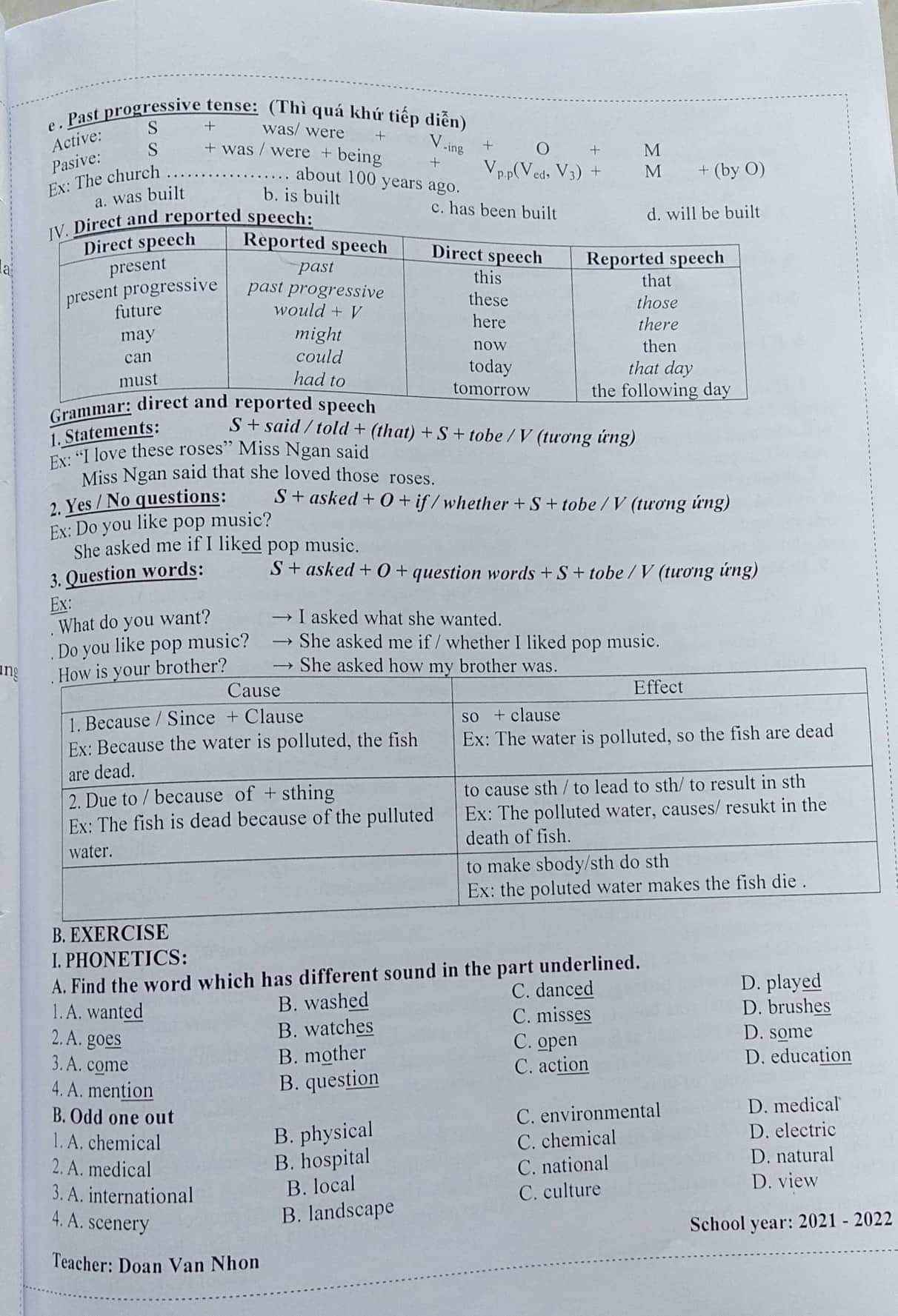


Ai rảnh có thể giúp em đc ko ạ? (Toàn trắc nghiệm thui ạ)

1 D
2 B
3 C
4 B
5 A
6 C
7 A
8 B
9 D
10 C
11 B
12 C
13 C
14 B
15 D
16 B
17 Children like the Mid-Autumn festival because they are given many toys and sweets
18 You shouldn't wear shorts when going to the pagoda
19 C => lived
20 C => because
Đúng 1
Bình luận (0)
MN có thể giúp em câu 45 đc ko ạ ?
Do \(M\in d\) nên M(1+2t; 1-t ; t)
MA+MB= \(\sqrt{4t^2+\left(t-1\right)^2+\left(t+1\right)^2}+\sqrt{\left(2t-1\right)^2+t^2+\left(t-1\right)^2}\)
\(=\sqrt{6t^2+2}+\sqrt{6t^2-6t+2}=\sqrt{6t^2+2+}\sqrt{6.\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}}\)
Chọn \(\overset{r}{u}=\left(\sqrt{6t};\sqrt{2}\right);\overset{r}{v}=\left(\sqrt{6}.\left(\dfrac{1}{2}-t\right);\dfrac{1}{\sqrt{2}}\right)\)
\(\Rightarrow\overset{r}{u}+\overset{r}{v}=\left(\dfrac{\sqrt{6}}{2};\dfrac{3}{\sqrt{2}}\right)\) , Ta có :
MA+MB=\(\left|\overset{r}{u}\right|+\left|\overset{r}{v}\right|\ge\left|\overset{r}{u}+\overset{r}{v}\right|=\sqrt{\dfrac{6}{4}+\dfrac{9}{2}}=\sqrt{6}\)
Dấu đẳng thức xảy ra <=> \(\overset{r}{u};\overset{r}{v}\) cùng hướng
\(\Leftrightarrow\dfrac{\sqrt{6t}}{\sqrt{6}\left(\dfrac{1}{2}-t\right)}=\dfrac{\sqrt{2}}{\dfrac{1}{\sqrt{2}}}\Leftrightarrow1=1-2t\)
\(\Leftrightarrow t=\dfrac{1}{3}\) . Vậy MA+MB nhỏ nhất
\(\Leftrightarrow M\left(\dfrac{5}{3},\dfrac{2}{3};\dfrac{1}{3}\right)\)
Vậy chọn D
Đúng 0
Bình luận (0)
MN có thể giúp em câu 46 đc ko ạ ?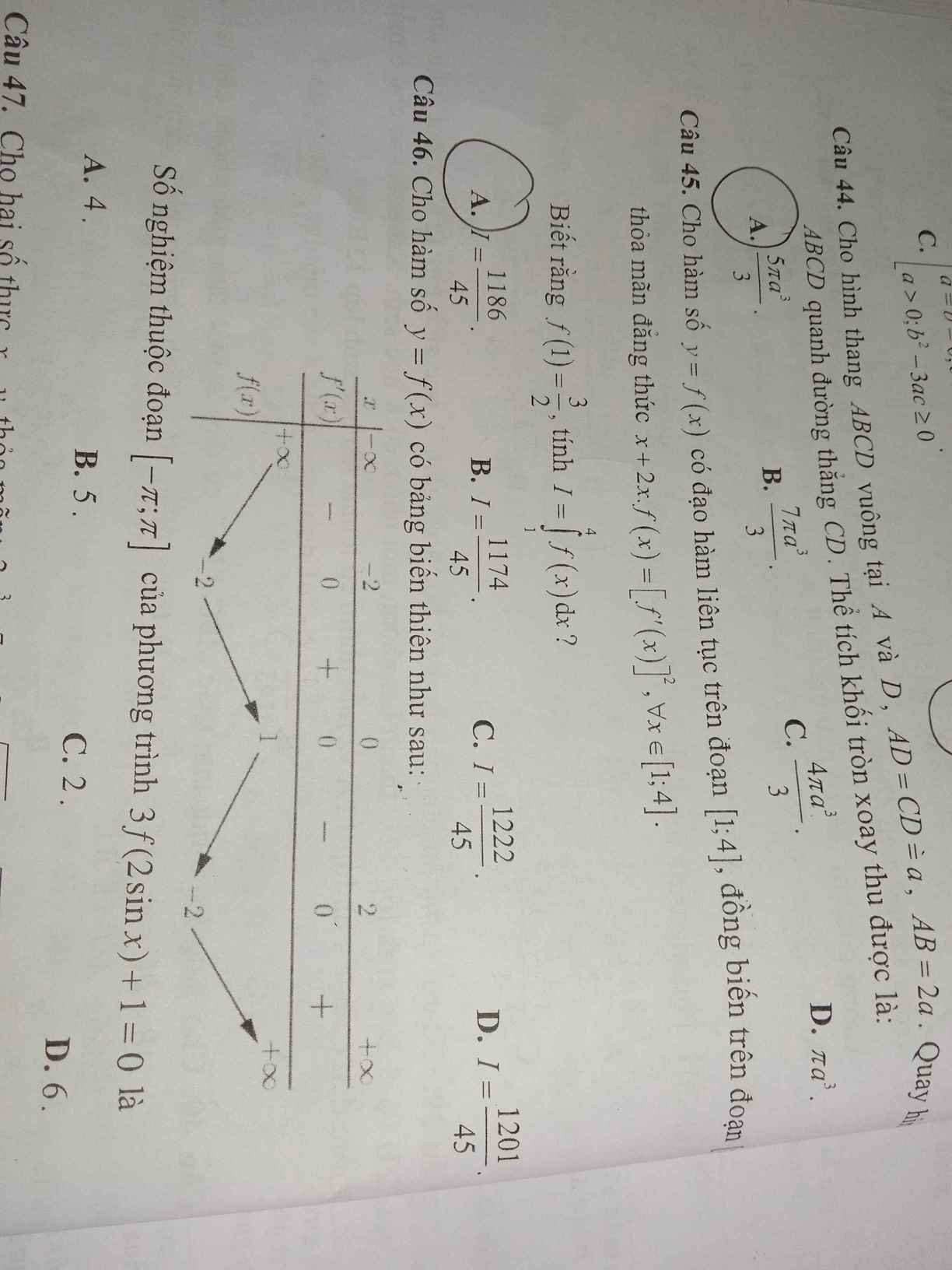
MN có thể giúp em câu 35 đc ko ạ ?
(SAB) và (SCD) có AB // CD => giao tuyến của chúng là 1 đường thẳng song song với AB và CD
Mà SD vuông góc với CD; SA vuông góc với AB nên góc giữa 2 mp (SAB) và (SCD) là góc giữa SA và SD hay là góc ASD
tan \(\widehat{ASD}\) = \(\dfrac{AD}{SA}\) = \(\dfrac{1}{\sqrt{3}}\)
=> \(\widehat{ASD}=30^{^o}\)
Đúng 1
Bình luận (0)
Giúp suốt mà bạn chẳng tick nun, mùng mọt ròi chơi đuy 33
Đúng 0
Bình luận (0)
MN có thể giúp em câu 29 đc ko ạ ?
+ số phần tử của không gian mẫu là: \(n\left(\pi\right)=C\overset{1}{6}.C\overset{1}{6}=36\)
+ gọi A bằng " Cả 2 lần xuất hiện mặt 6 chấm "
số phần tử của biến cố A là n(A) =1
Xác xuất biến cố A là P(A) = \(\dfrac{n\left(A\right)}{n\left(\pi\right)}=\dfrac{1}{36}\)
Vậy chọn A
Đúng 0
Bình luận (0)
Có thể giúp em giải 2câu này đc ko ạ 😭
Mn có thể giúp em câu 40 này đc ko ạ 
\(g'\left(x\right)=3.f'\left(3x\right)+9=0\Rightarrow f'\left(3x\right)=-3\Rightarrow\left[{}\begin{matrix}3x=-1\\3x=0\\3x=1\\3x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=0\\x=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\) Trên \(\left[-\dfrac{1}{3};\dfrac{1}{3}\right]\) hàm \(g\left(x\right)\) đạt cực đại tại \(x=0\) và cực tiểu tại \(x=-\dfrac{1}{3};\dfrac{1}{3}\)
\(\Rightarrow g\left(x\right)_{max}=g\left(0\right)=f\left(0\right)\)
Đúng 0
Bình luận (0)






