Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M ( - 1 ; 7 ) và N ( 5 ; - 7 ) . Gọi x 1 ; x 2 ; x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Oy xuống dưới 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Chọn A.
Theo lý thuyết, ta chọn câu A.
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là
A. (0;-1)
B. 5 2 ; 8
C. 0 ; - 1 v à 5 2 ; 9
D. 5 2 ; 9
f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
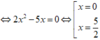
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()
Cho hàm số f(x)=x+1với x∈R.
a) Giả sử x0∈R.Hàm số f(x)
có liên tục tại điểm x0 hay không?
b) Quan sát đồ thị hàm số f(x)=x+1 với x∈R (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
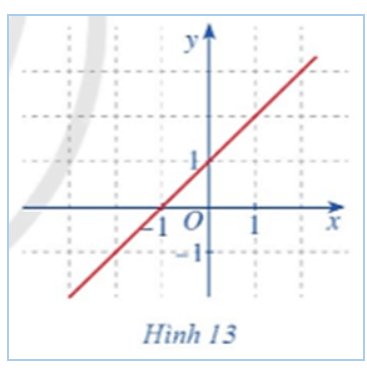
a: f(x0)=x0+1
\(\lim\limits_{x\rightarrow x0}f\left(x\right)=x_0+1\)=f(x0)
=>HS f(x) liên tục tại điểm x0
b: Đồ thị hàm số là một đường thẳng liền mạch với mọi x thực
Mọi người giúp mk câu này vs ạ
Bài 8. Cho hàm số y = f(x) = x -2
a)Tính f(-1) ; f(0)
b)Tìm x để f(x) = 3
c)Điểm nào sau đây thuộc đồ thị của hàm số y = f(x) = x -2 : A(1;0) ; B(-1;-3) C(3;-1)
Bài 9. a) Vẽ đồ thị của hàm số y = - 2x
b) Điểm sau điểm nào thuộc đồ thị hàm số: A (-2; 4); B(-1; -2)
Bài 10: Cho hàm số y = f(x) = ax (a # 0)
a)Tìm a biết đồ thị hàm số đi qua điểm A( 1; -3)
b)Vẽ đồ thị ứng với giá trị a vừa tìm được
Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.
Bài 8:
a. y = f(x) = -1- 2= -3
y = f(x) = 0-2= -2
b. cho y = f(x)= 3
ta có: 3=x-2 => x-2=3
x= 3+2
x= 5
c. điểm B
câu 1: cho hàm số y=ax+b
Xác định giá trị a và b biết đồ thị hàm số đi qua điểm M; m(2;5) và N(1/3;0)
câu 2: cho hàm số:y=f(x)=-2x; g(x)=x-1
a, tính f(3); g(-2)
b, tìm tung độ của điểm A thuộc đồ thị hàm số của điểm A thuộc đồ thị hàm số f(x) có hoành độ là 1/2
c.tính hoành độ của điểm B thộc đồ thị hàm số g(x)có tung độ là -3
d, điểm C(1/3;-2/3) có thuộc đồ thị hàm số f(x); g(x) không
Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2
1,04 m
tk mk nha
mk sẽ tk lại
hứa mà
1.
cho hàm số y= f(x)= x-2
điểm nào sau đây thuộc đồ thị của hàm số y=f(x)=x-2
A(1;0) ; B(-1;-3) ; C(-3;-1)
2.vẽ đồ thị hàm số y=3x lên mặt phẳng tọa độ Oxy?
3.cho hàm số y=f(x)=ax (a \(\ne\)o)
a. tìm a biết đồ thị hàm số đi qua điểm A(1;-2)
b. Vẽ đồ thị ứng với giá trị a vừa tìm đc
các bn làm ơn giúp mk giải bài toán này ik mk đag cần nó gấp :(
mình cũng chả vt
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
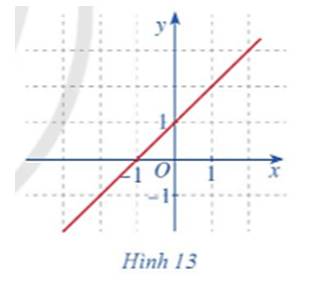
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)