Trong không gian với hệ tọa độ Oxyz, cho u → = 2 j → - 4 i → + 6 k → . Tìm tọa độ của vectơ u → ?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho u → = ( - 2 ; 3 ; 0 ) ; v → = ( 2 ; - 2 ; 1 ) , tọa độ của véc tơ w → = u → - 2 v → là
A. (-6;7;-2)
B. (6;-8;1)
C. (6;3;0)
D. (-6;3;0)
Đáp án A
Ta có: w → = u → - 2 v → = - 2 ; 3 ; 0 - 2 2 ; - 2 ; 1 = - 6 ; 7 ; - 2
Trong không gian với hệ tọa độ O ; i → ; j → ; k → cho u → = 2 i → - j → + k → . Tính u → ?
A. u → = 6
B. u → = 2
C. u → = 4
D. u → = 5
Trong không gian với hệ tọa độ O ; i → ; j → ; k → cho u → = 2 i → - j → + k → . Tính u → ?
![]()
![]()
![]()
![]()
cho mình hỏi vs
câu 1 trong không gian hệ trục tọa độ Oxyz cho mặt phẳng (A) đi qua hai điểm A( 2;-1;0) và có vecto pháp tuyến n (3:5:4)viết phương trình mặt cầu
câu 2 trong không gian với hệ trục tọa độ Oxyz cho mặt cầu (S) có tâm I(2;-3:7) và đi qua điểm M(-4:0;1) viết phương trình mặt cầu
Trong không gian với hệ tọa độ Oxyz cho u → = ( 1 ; 0 ; 1 ) v → = ( 0 ; 1 ; - 2 ) là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
=(2;-3;1) và ![]() =(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3
=(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3![]() .
.
A.![]() =(-7;6;-10)
=(-7;6;-10)
B.![]() =(-7;6;10)
=(-7;6;10)
C.![]() =(7;6;10)
=(7;6;10)
D.![]() =(-7;-6;10)
=(-7;-6;10)
Đáp án B
Ta có -2![]() +3
+3![]() =(-7;6;10), nên
=(-7;6;10), nên ![]() =(-7;6;10).
=(-7;6;10).
Trong không gian với hệ tọa độ Oxyz cho vectơ u → = 2 ; - 1 ; 2 và vectơ đơn vị v → thỏa mãn u → - v → = 4 Độ dài của vectơ u → + v → bằng
A. 1
B. 2
C. 3
D. 4
Theo giả thiết, ta có 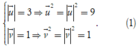
Từ
u
→
-
v
→
=
4
, suy ra ![]()
Kết hợp (1) và (2) ta được ![]()
Khi đó ![]()
Vậym | u → + v → | = 2
Chọn B.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A − 1 ; 2 ; 3 . Gọi B là điểm thỏa mãn AB → = 2 i → − j → . Tìm tọa độ của điểm B.
A. B 1 ; 1 ; 3
B. B - 1 ; - 1 ; 3
C. B 1 ; 3 ; 1
D. B 1 ; 3 ; 3
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ a → = 2 ; - 3 ; 1 và b → = - 1 ; 0 ; 4 . Tìm tọa độ véctơ u → = - 2 a → + 3 b → .
A. u → = - 7 ; - 6 ; 10
B. u → = - 7 ; 6 ; 10
C. u → = 7 ; 6 ; 10
D. u → = - 7 ; 6 ; - 10
Đáp án B
Ta có u → = - 2 a → + 3 b → = - 7 ; 6 ; 10 .