Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho A(1 ;-2 ;0), B(0 ;2 ;0), C(2 ;1 ;3). Tọa độ điểm M thỏa mãn
M
A
→
-
M
B
→
+
M
C
→
0
→
là: A. (3;2;-3) B. (3;-2;3) C. (3;-2;-3) D. (3;2;3)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(1 ;-2 ;0), B(0 ;2 ;0), C(2 ;1 ;3). Tọa độ điểm M thỏa mãn M A → - M B → + M C → = 0 → là:
A. (3;2;-3)
B. (3;-2;3)
C. (3;-2;-3)
D. (3;2;3)
Trong không gian với hệ tọa độ Oxyz, cho
a
→
(
−
3
;
5
;
2
)
,
b
→
(
0
;
−
1
;
3
)
,
c
→
(
1
;
−
1
;
1
)
thì tọa độ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = ( − 3 ; 5 ; 2 ) , b → = ( 0 ; − 1 ; 3 ) , c → = ( 1 ; − 1 ; 1 ) thì tọa độ v → = 2 a → − 3 b → + 15 c → là
A. v → = ( 9 ; 2 ; 10 )
B. v → = ( 9 ; - 2 ; 10 )
C. v → = ( - 9 ; 2 ; 10 )
D. v → = ( 9 ; - 1 ; 10 )
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
2
x
-
z
+
1
0
. Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - z + 1 = 0 . Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng đi qua hai điểm A(1; 1; 2) và B(2; -1; 0) là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng đi qua hai điểm A(1; 1; 2) và B(2; -1; 0) là:
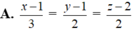
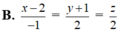
![]()
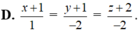
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình
(
S
)
:
x
2
+
y
2
+
z
2
-
4
x
+
2
y
-
6
z
+
1
0
. Tọa độ tâm mặt cầu là A. (-4;2;-6) B. (2;-1;3) C. (-2;1;-3) D. (4;-2;-6)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình ( S ) : x 2 + y 2 + z 2 - 4 x + 2 y - 6 z + 1 = 0 . Tọa độ tâm mặt cầu là
A. (-4;2;-6)
B. (2;-1;3)
C. (-2;1;-3)
D. (4;-2;-6)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) 2x+y-1=0. Mặt phẳng (P) có 1 vecto pháp tuyến là
A. (-2;-2;1)
B. (2;1;-1)
C. (1;2;0)
D. (2;1;0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y -2z - 1 0 và đường thẳng d:
x
-
2
1
y
-
2
1
z
-
2
. Tọa độ giao điểm của d và là B. (1;0;0) C. (2;2;0)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y -2z - 1 = 0 và đường thẳng d: x - 2 1 = y - 2 1 = z - 2 . Tọa độ giao điểm của d và là
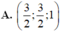
B. (1;0;0)
C. (2;2;0)
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
![]()
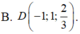
![]()
![]()


