Cho ∫ 0 1 x f ' ( x ) d x = 1 và f(1)=10. Tích phân ∫ 0 1 f ( x ) d x bằng:
A. 8.
B. 11.
C. 10.
D. 9.
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
1,Cho đa thức bậc 4 f(x) biết f(1)=f(2)=f(3)=0, f(4)=6 và f(5)=72. Tìm dư f(2010) khi chia cho 10
2,Cho đa thức bậc 4 f(x) có hệ số bậc cao nhất bằng 1 và f(1)=10,f(2)=20 và f(3)=30. Tính f(10)+f(-6)
3,Tìm đa thức f(x) biết rằng f(x) chia cho x-3 thì dư 2, f(x) chia cho x+4 thì dư 9 còn f(x) chia cho x^2+x-12 thì được thương là x^2+3 và còn dư.
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
a)A={nϵN/n(n+1)≤15}
b)B={3k-1/kϵZ,-5≤k≤3}
c)C={xϵZ//x/<10}
d)D={xϵQ/x2-3x+1=0}
e)E={xϵZ/2x3-5x2+2x=0}
f)F={xϵN/x<20 và x chia hết cho 3}
\(a,A=\left\{0;1;2;3;4\right\}\\ b,B=\left\{-16;-13;-10;-7;-4;-1;2;5;8\right\}\\ c,C=\left\{-9;-8;-7;...;7;8;9\right\}\\ d,x^2-3x+1=0\\ \Delta=9-4=5\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{5}}{2}\\x=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\\ \Leftrightarrow D=\left\{\dfrac{3-\sqrt{5}}{2};\dfrac{3+\sqrt{5}}{2}\right\}\)
\(e,2x^3-5x^2+2x=0\\ \Leftrightarrow x\left(x-2\right)\left(2x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow E=\left\{0;2\right\}\\ f,F=\left\{0;3;6;9;12;15;18\right\}\)
Thầy cho em hỏi ạ:
1,Cho đa thức bậc 4 f(x) biết f(1)=f(2)=f(3)=0, f(4)=6 và f(5)=72. Tìm dư f(2010) khi chia cho 10
2,Cho đa thức bậc 4 f(x) có hệ số bậc cao nhất bằng 1 và f(1)=10,f(2)=20 và f(3)=30. Tính f(10)+f(-6)
3,Tìm đa thức f(x) biết rằng f(x) chia cho x-3 thì dư 2, f(x) chia cho x+4 thì dư 9 còn f(x) chia cho x^2+x-12 thì được thương là x^2+3 và còn dư.
1)
Đặt \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e.\)( a khác 0 )
Ta có:
\(f\left(1\right)=a+b+c+d+e=0\) (1)
\(f\left(2\right)=16a+8b+4c+2d+e=0\) (2)
\(f\left(3\right)=81a+27b+9c+3d+e=0\) (3)
\(f\left(4\right)=256a+64b+16c+4d+e=6\) (4)
\(f\left(5\right)=625a+125b+25c+5d+e=72\) (5)
\(A=f\left(2\right)-f\left(1\right)=15a+7b+3c+d=0\)
\(B=f\left(3\right)-f\left(2\right)=65a+19b+5c+d=0\)
\(C=f\left(4\right)-f\left(3\right)=175a+37b+7c+d=6\)
\(D=f\left(5\right)-f\left(4\right)=369a+61b+9c+d=72-6=66\)
\(E=B-A=50a+12b+2c=0\)
\(F=C-B=110a+18b+2c=6\)
\(G=D-C=194a+24b+2c=66-6=60\)
Tiếp tục lấy H=F-E; K=G-F; M=H-K
Ta tìm được a
Thay vào tìm được b,c,d,e
1. gọi đa thức cần tìm là f(x) =a.x^4+b.x^3+c.x^2+dx+e
có f(1)=f(2)=f(3) = 0 nên x=1,2,3 la nghiệm của f(x) = 0 vậy f(x) có thể viết dưới dạng f(x) = (x-1)(x-2)(x-3)(mx+n)
thay f(4)=6 và f(5)=72 tìm được m =2 và n= -7
Vậy đa thức f(x) =(x-1)(x-2)(x-3)(2x-7) => e = (-1).(-2).(-3).(-7) = 42
Với x=2010 thì (a 2010^4+b.2010^3+c.2010^2+d.2010 ) luôn chia hết 10 vậy số dư f(2010) chia 10 = số dư d/10 = 2 (42 chia 10 dư 2).
2. Thiếu dữ liệu
3. đa thức f(x) chia đa thức (x-3) có số dư là 2 =>bậc f(x) = bậc (x-3)=1 và f(x) = m.(x-3) +2=mx+2-3m (1)
...........................................(x+4)...................9..........................................f(x) = n(x+4) + 9=nx+4n+9 (2)
để (1)(2) cùng xảy ra thì m=n và (2-3m)=(4n+9) => m = n = -1 khi đó đa thức f(x) = -x +5
Không hiếu dữ liệu cuối f(x) chia 1 đa thức bậc 2 lại có thương là 1 đa thức bậc 2? => vô lý
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) – f(0) = 2. Tính I = ∫ 0 1 f ( x ) d x
A. I = -12.
B. I = 8.
C. I = 12.
D. I = -8.
Chọn D.
Đặt u = x + 1 d v = f ' ( x ) d x ⇒ d u = d x v = ∫ f ' ( x ) d x
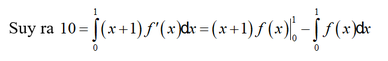
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
Cho hàm số f(x) ={\(\dfrac{-2\left(x-3\right)}{\sqrt{x^2-1}}\)\(\dfrac{-1\le x< 1}{x\ge1}\)giá trị của f(-1), f(1) lần lượt là
A. 0 và 8 B. 8 và 0 C. 0 và 0 D. 8 và 4
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8