Tìm tất cả các giá trị thực của tham số m để phương trình 3 2 x - 1 + 2 m 2 - m - 3 = 0 có nghiệm
A. m ∈ - 1 ; 3 2
B. m ∈ 1 2 ; + ∞
C. m ∈ 0 ; + ∞
D. m ∈ - 1 ; 3 2
ĐỀ THI HỌC KỲ I
Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1)
Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm
Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Đáp án C
Phương pháp:

![]() phương trình trở thành
phương trình trở thành
![]()
![]()
![]()
=> Hàm số đồng biến trên khoảng [2;+∞)
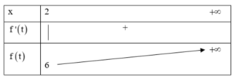
Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥1?
A. m ϵ [2;+∞).
B. m ϵ [3;+∞).
C. m ϵ (-∞;2].
D. m ϵ (-∞;3].
tìm tất cả các giá trị thực của tham số m để phương trình \(^{x^2-2x+\sqrt{-x^2+2x}-3+m=0}\) có nghiệm
Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)
\(\Rightarrow-t^2+t-3+m=0\)
\(\Leftrightarrow t^2-t+3=m\)
Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)
\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
tìm tất cả các giá trị thực của tham số m để phương trình x-4√(x+3 ) + m = 0 có 2 nghiệm phân biệt
\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 5 x - 1 . log 2 2 . 5 x - 2 ≥ m có nghiệm x ≥ 1
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Đáp án C.
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m
Đặt t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )
Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m
Với f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0 với t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6
Do đó theo bài ra để bất phương trình có nghiệm x ≥ 1 thì m ≤ min f ( t ) ⇔ m ≤ 6
Câu 1. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
m x m 4 3 6
vô nghiệm.
A.
m 1.
B.
m 2.
C.
m 2.
D.
m 2.
Câu 2. Tìm tất cả các giá trị thực của tham số
m
để phương trình
mx m 0
vô nghiệm.
A.
m.
B.
m 0 .
C.
m .
D.
m .
Câu 3. Tìm giá trị thực của tham số
m
để phương trình
2 2
m m x m m 5 6 2
vô nghiệm.
A.
m 1.
B.
m 2.
C.
m 3.
D.
m 6.
Câu 4. Cho phương trình
2
m x m x m 1 1 7 5
. Tìm tất cả các giá trị thực của tham số
m
để phương trình đã cho vô
nghiệm.
A.
m 1.
B.
m m 2; 3.
C.
m 2.
D.
m 3.
Câu 6. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 4 2 m x m
có nghiệm duy nhất.
A.
m 1.
B.
m 2.
C.
m 1.
D.
m 2.
Trang 24
Câu 11. Tìm tất cả các giá trị thực của tham số để phương trình có nghiệm đúng với mọi thuộc
A. B. C. D.
Vấn đề 2. SỐ NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI
Câu 16. Phương trình
2
ax bx c 0
có nghiệm duy nhất khi và chỉ khi:
A.
a 0.
B.
0
0
a
hoặc
0
.
0
a
b
C.
abc 0.
D.
0
.
0
a
Câu 17. Số 1
là nghiệm của phương trình nào trong các phương trình sau?
A.
2
x x 4 2 0.
B.
2
2 5 7 0. x x
C.
2
3 5 2 0. x x
D.
3
x 1 0.
Câu 20. Phương trình vô nghiệm khi:
A. B. C. D.
Câu 22. Phương trình có nghiệm kép khi:
A. B. C. D.
m
2 m x m 1 1 x .
m 1. m 1. m 1. m 0. 2 m x mx m 1 2 2 0 m 2. m 2. m 2. m 2. 2 m x x – 2 2 –1 0 m m 1; 2. m 1. m 2. m 1.
Trang 25
Câu 23. Phương trình có nghiệm duy nhất khi:
A. B. C. D.
Câu 24. Phương trình có nghiệm duy nhất khi:
A. B. C. D.
Câu 25. Phương trình có nghiệm kép khi:
A. B. C. D.
Vấn đề 3. DẤU CỦA NGHIỆM PHƯƠNG TRÌNH BẬC HAI
Câu 41. Phương trình
2
ax bx c a 0 0
có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
.
P 0
B.
0
.
P 0
C.
0
.
S 0
D.
0
.
S 0
Câu 42. Phương trình
2
ax bx c a 0 0
có hai nghiệm âm phân biệt khi và chỉ khi:
A.
0
.
P 0
B.
0
0.
0
P
S
C.
0
0.
0
P
S
D.
0
.
S 0
2 mx x m 6 4 3 m . m 0. m . m 0. 2 mx m x m – 2 1 1 0 m 0. m 1. m m 0; 1. m 1. 2 m x m x m 1 – 6 1 2 3 0 m 1. 6
1;
7
m m
6
.
7
m
6
.
7
m
Trang 26
Câu 43. Phương trình
2
ax bx c a 0 0
có hai nghiệm dương phân biệt khi và chỉ khi:
A.
0
.
P 0
B.
0
0.
0
P
S
C.
0
0.
0
P
S
D.
0
.
S 0
Câu 44. Phương trình
2
ax bx c a 0 0
có hai nghiệm trái dấu khi và chỉ khi:
A.
0
.
S 0
B.
0
.
S 0
C.
P 0.
D.
P 0.
Câu 45. Phương trình
2
x mx 1 0
có hai nghiệm âm phân biệt khi:
A.
m 2.
B.
m 2.
C.
m 2.
D.
m 0.
Tìm tất cả các giá trị thực của tham số m để phương trình e 3 m + e m = 2 x + 1 - x 2 1 + x 1 - x 2 có nghiệm.
A. [ 1 2 ln 2 ; + ∞ )
B. 0 ; 1 2 ln 2
C. ( - ∞ ; 1 2 ln 2 ]
D. 0 ; 1 e
ĐKXĐ:
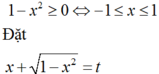
ta có
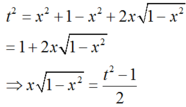
Ta có:
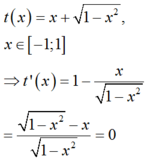
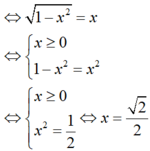
BBT:
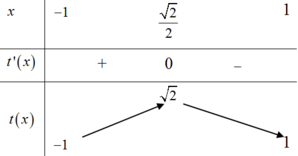
Từ BBT ta có:
t ∈ - 1 ; 2
Khi đó phương trình trở thành:
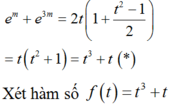
ta có
![]()
Hàm số đồng biến trên R Hàm số đồng biến trên t ∈ - 1 ; 2 .
Từ
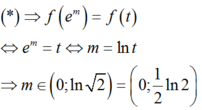
Chọn B.