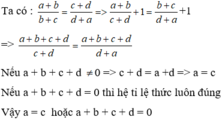Chứng minh rằng nếu a b < c d ( b > 0 , d > 0 ) thì: a b < a + c b + d < c d
PB
Những câu hỏi liên quan
Chứng minh rằng nếu a+b/b+c =c+d/d+a (c+d khác 0) thì a=c và a+b+c+d=0
Chứng minh rằng nếu a/b < c/d (b>0 ,d>0 ) thì a/b < a+c/b+d < c/d
Ta có : \(\frac{a}{b}0\) \(\left(1\right)\)
vì \(ad\)\(
Đúng 0
Bình luận (0)
Chứng minh rằng : Nếu a/b < c/d (b>0,d>0) thì a/b <a+c/b+d<c/d
Ta có:a/b<c/d =>ad<bc (1)
Thêm ab vào (1) ta đc:
ad+ab<bc+ab hay a(b+d)<b(a+c) =>a/b<a+c/b+d (2)
Thêm cd vào 2 vế của (1), ta lại có:
ad+cd<bc+cd hay d(a+c)<c(b+d) => c/d>a+c/b+d (3)
Từ (2) và (3) suy ra:a/b<a+c/b+d<c/d
Đúng 0
Bình luận (0)
chứng minh rằng nếu a/b < c/d ( b > 0 , d > 0 thì a/b < a + c/ b+d < c / d
ta có:a/b<c/d nên ad<bc
(1)ab+ad<ab+bc=a(b+d)<b(a+c)=>a/b<a+c/b+d(thêm ab vào hai vế)
(2)ad+cd<bc+cd=(a+c)d<(b+d)c=>a+c/b+d<c/d(thêm cd vào hai vế)
từ(1)và(2)ta có:a/b<a+c/b+d<c/d
Đúng 0
Bình luận (0)
hãy chứng minh rằng, nếu:
a/b<c/d(b>0,d>0) thì : a/b<a+c/b+d<c/d
Chứng minh rằng nếu a + b/ b+ c = c+ d/ d+ a thì a= c hoặc a+ b+ c+ d= 0 (với c+ d# 0)Cho x/a+2b+c= y/2a+y-z = z/4a-4b+c. Chứng minh rằng : a/x+2y+z=b/ 2x+y-z = c/ 4x- 4y+ c
Xem chi tiết
( với abc # 0 và các mẫu đều khác 0)
Chứng minh rằng: Nếu a + b b + c = c + d d + a (c + d ≠ 0) thì a = c hoặc a = b + c + d = 0
chứng minh rằng nếu a phần b < c phần d ( b< 0 , d>0 ) thi : a phần b < a+c phần b+d < c phần d
chứng minh rằng nếu a+b/c+d=b+c/d+a với a+b+c+d khác 0 thì a=c
\(\frac{a+b}{c+d}=\frac{b+c}{d+a}\)
<=>\(\frac{a+b}{c+d}+1=\frac{b+c}{d+a}+1\)
<=> \(\frac{a+b+c+d}{c+d}=\frac{a+b+c+d}{d+a}\)
<=> \(\frac{a+b+c+d}{c+d}-\frac{a+b+c+d}{d+a}=0\)
<=> \(\left(a+b+c+d\right)\left(\frac{1}{c+d}-\frac{1}{d+a}\right)=0\)
<=> \(\orbr{\begin{cases}a+b+c+d=0\\\frac{1}{c+d}-\frac{1}{d+a}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a+b+c+d=0\\c=a\end{cases}\left(đpcm\right)}}\)
Đúng 1
Bình luận (0)
Bài 1:Cho 2 soos hữu tỷ a/b , c/d (b > 0 , d > 0) . Chứng minh rằng a/b < c/d nếu a/d < b/c và ngược lại.
Bài 2: Chứng minh nếu a/b < c/d (b > 0, d >0) thì : a/b < a+c/ b+d < c/d.
giúp mình với mình đang cần gấp lắm
B1: Ta có :a/b < c/d
=>ad/bd < bc/ba
=>ad < bc
Đúng 0
Bình luận (0)