Biết tập nghiệm của bất phương trình l o g 2 1 3 + 4 l o g 1 3 x + 3 ≤ 0 là đoạn [a;b]. Giá trị của b a là
A. 1 9
B. 1 6
C. 6
D. 9
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - 2y + 3 \le 0\\x + 3y > - 2\\x \le 0\end{array} \right.\)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau.
Bước 1: Mở trang Geoebra
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
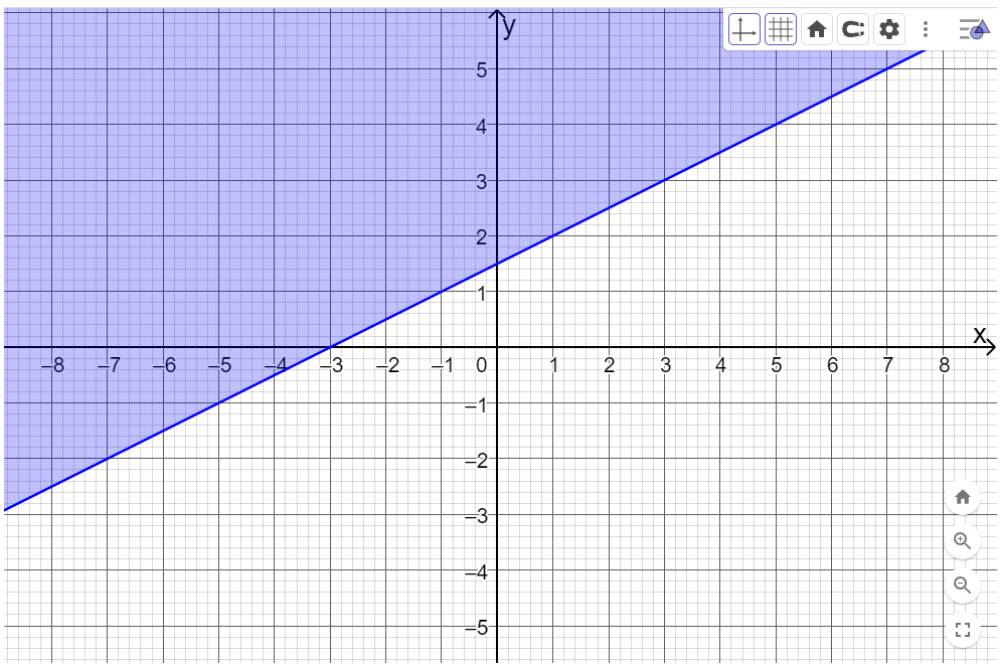
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
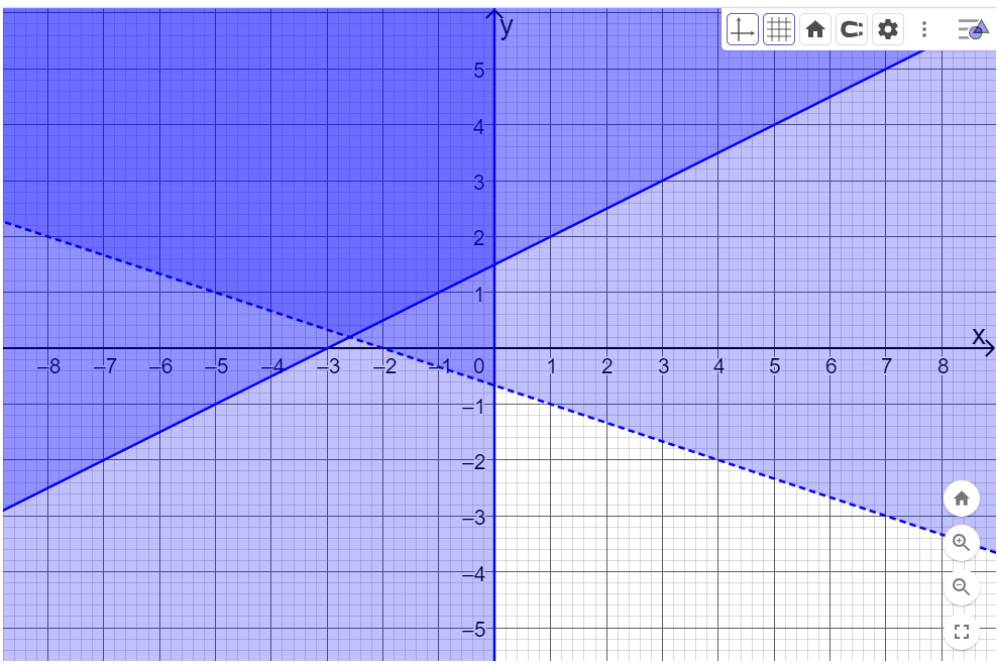
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.
tìm m để x=7 là nghiệm của bất phương trình(m-1)x/x-2 -3>2x-24
tìm x biết 4x-3/x+2>5
tìm tập nghiệm của bất phương trình 1-3x/2 -3<x- x+1/4
1) Điều kiện của m để bất phương trình \(\left(m^2-m\right)x\ge1-m\) có nghiệm là :
2) Hệ bất phương trình \(\left\{{}\begin{matrix}2x+7< 8x-1\\-2x+m+5\ge0\end{matrix}\right.\) vô nghiệm khi:
3) Hệ bất phương trình \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge x^2+7x+1\\2m-5x\le8\end{matrix}\right.\) vô nghiệm khi:
4) Tập nghiệm của bất phương trình \(\left(x-1\right)\left(x^2-3x+2\right)< 0\) là :
5) Tập nghiệm của bất phương trình \(\left(x+3\right)\left(x^2+4x+3\right)\ge0\) là :
6) Tập nghiệm của bất phương trình \(\frac{x^2-x+1}{x-1}\ge0\) là :
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
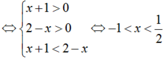
1.Bất phương trình \(\dfrac{x}{(x-1)²}\)≥0 có tập nghiệm là?
******
2.Bất phương trình \(\dfrac{3x+1}{2}\)<\(\dfrac{2x-1}{4}\) có tập nghiệm là?
******
3.Biết 0<a<b, bất đẳng thức nào là sai?
A. a³<b³
B. \(\dfrac{1}{a}<\dfrac{1}{b}\)
C. a²<b²
******
4.Với giá trị nào của m thì phương trình (m-3)x²+(m+3)x-(m+1)=0?
******
5.Bất phương trình x²≥1 tương đương với bất phương trình nào?
A. |x|>1
B. x≤-1
C. |x|≥1
******
6.Bảng xét dấu sau là của biểu thức nào?
| x | -∞ | \(-\dfrac{1}{3}\) | +∞ | ||
| f(x) | - | 0 | - |
******
7.Tập nghiệm của bất phương trình |x²+x-12|<x²+x+12 là?
******
8.Giải bất phương trình (x-1)(2+x)>0
Câu 1:
ĐK: $x\neq 1$
Với $x\neq 1$ thì $(x-1)^2>0$. Do đó để $\frac{x}{(x-1)^2}\geq 0$ thì $x\geq 0$
Kết hợp với ĐKXĐ ta suy ra tập nghiệm là \(x\in [0;+\infty)\setminus \left\{1\right\}\)
Câu 2:
\(\frac{3x+1}{2}< \frac{2x-1}{4}\Leftrightarrow 2(3x+1)< 2x-1\)
\(\Leftrightarrow 4x< -3\Leftrightarrow x< \frac{-3}{4}\)
Tập nghiệm \(x\in (-\infty; -\frac{3}{4})\)
Câu 3:
$0< a< b$ thì $\frac{1}{a}> \frac{1}{b}$. Đáp án B sai.
Câu 4: Đề thiếu
Câu 5:
$x^2\geq 1\Leftrightarrow |x|^2\geq 1$
$\Leftrightarrow (|x|-1)(|x|+1)\geq 0$
$\Leftrightarrow |x|-1\geq 0$ (do $|x|+1>0$)
$\Leftrightarrow |x|\geq 1$
Đáp án C
Câu 6:
Từ đề bài ra suy ra \(\left\{\begin{matrix} f(-\frac{1}{3})=0\\ f(x)< 0, \forall x\in (-\infty; -\frac{1}{3})\\ f(x)< 0, \forall x\in (\frac{-1}{3}; +\infty)\end{matrix}\right.\)
Biểu thức có tính chất như thế này là $y=-|3x+1|$
Câu 7:
$|x^2+x-12|=|(x-3)(x+4)|$
Nếu $x\geq 3$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Nếu $3> x> -4(1)$ thì $(x-3)(x+4)< 0$
$\Rightarrow |x^2+x-12|=-(x^2+x-12)$
BPT trở thành: $-(x^2+x-12)< x^2+x+12$
$\Leftrightarrow 2(x^2+x)>0\Leftrightarrow x>0$ hoặc $x< -1$
Kết hợp với $(1)$ suy ra $3>x>0$ hoặc $-1> x> -4$
Nếu $x\leq -4$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Vậy BPT có nghiệm $x\in (+\infty; 0)$ hoặc $x\in (-\infty; -1)$
Bài 2: Giải các bất phương trình sau và biểu diện tập nghiệm của mỗi bất phương trình trên một trục số
a. 2x – 3 > 3(x – 2) b.12x+1/12 <_ 9x +1/3 - 8x +1/4
/ : phần
a: 2x-3>3(x-2)
=>2x-3>3x-6
=>-x>-3
hay x<3
b: \(\dfrac{12x+1}{12}< =\dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
=>12x+1<=36x+4-24x-3
=>12x+1<=12x+1(luôn đúng)
Tập nghiệm của bất phương trình: ( x - 1 ) 2 + ( x - 3 ) 2 + 15 < x 2 + ( x - 4 ) 2 là?
A. S = x > 0
B. x < 0
C. S = R
D. S = Ø
Hãy cho biết vế trái, vế phải và tập nghiệm của bất phương trình x > 3, bất phương trình 3 < x và phương trình x = 3.
- Bất phương trình x > 3 có VT = x; VP = 3
Nghiệm của bất phương trình x > 3 là tập hợp các số lớn hơn 3, {x|x > 3}
- Bất phương trình 3 < x có VT = 3; VP = x
Nghiệm của bất phương trình 3 < x là tập hợp các số lớn hơn 3, {x|x > 3}
- Phương trình x = 3 có VT = x; VP = 3
Nghiệm của phương trình x = 3 là 3.