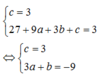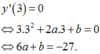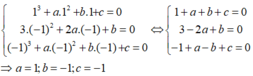Cho a,b,c∈R sao cho hàm số y=x 3 + ax 2 + bx + c đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 16 .
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 5 ) 2 = 64 .
C. x 2 + y 2 + ( z + 5 ) 2 = 36 .
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 .