Tìm m để đồ thị hàm số y = x 3 − 3 mx 2 + 2 có hai điểm cực trị A; B sao cho tam giác OAB có diện tích bằng 1
A. m = ± 2
B. m = ± 5
C. m = ± 1 5
D. m = ± 1
Mọi người giúp mình với ạ!!! Mình cảm ơn rất nhiều!!!
1, Viết phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số:
\(y=x^3-6x^2-3x+2\)
2, Cho hàm số: \(y=x^3-x^2+mx\)
Tìm m để đồ thị hàm số có các điểm cực đại, cực tiểu: A, B sao cho Δ OAB vuông góc tại O.
Bài 1: Cho hàm số \(y=x^3+3x^2+mx+m-2\) (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành
Bài 2: Cho hàm số \(y=\dfrac{2x-2}{x+1}\) . Tìm m để đường thẳng d: \(y=2x+m\) cắt đồ thị (C) tại 2 điểm phân biệt A, B sao cho AB=\(\sqrt{5}\)
Bài 3: Cho hàm số \(y=\dfrac{1}{3}x^3-mx^2+2(m-1)x-3\) (m là tham số) có đồ thị là (Cm) . Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tung
Bài 4: Cho hàm số \(y=-x^3+2(m-1)x^2-(m^2-3m+2)x-4\)
(m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung
Bài 5: Cho hàm số \(y=-x^3+3x^2+3(m^2-1)x-3m^2-1\) (1). Tìm m để hàm số (1) có cực đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O
1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)
3.
\(y'=x^2-2mx+2\left(m-1\right)\)
Hàm có 2 điểm cực trị nằm về cùng phía đối với trục tung khi và chỉ khi \(y'=0\) có 2 nghiệm pb cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-2\left(m-1\right)>0\\ac=1.2\left(m-1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-2m+2>0\left(\text{luôn đúng}\right)\\m>1\end{matrix}\right.\)
\(\Leftrightarrow m>1\)
tìm m để đồ thị hàm số
1) \(y=mx^4+\left(m^2-9\right)x^2+10\) có 3 điểm cực trị
2) \(y=mx^4+\left(2m+1\right)x^2+1\) có một điểm cực tiểu
3) \(y=\left(m+1\right)x^4-mx^2+\dfrac{3}{2}\) chỉ có cực tiểu mà không có cực đại
Cho hàm số \(y=x^4-2m\left(m+1\right)x^2+m^2\) với m là tham số thực.
a) Tìm m để đồ thị hàm số trên có 3 cực trị tạo thành 3 đỉnh của tâm giác vuông
b) Tìm m để đồ thị hàm số trên có 3 cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Cho hàm số y = x 3 - x 2 + m x - 2 có đồ thị (C). Tìm m để đồ thị (C) có hai điểm cực trị A, B và đường thẳng AB vuông góc với đường thẳng d : y = 1 2 x + 1
A. m = 8 3
B. m = 1
C. m = - 8 3
D. m = - 26 3
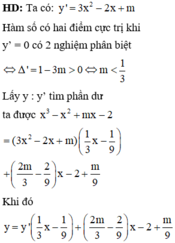
Phương trình đường thẳng đi qua 2 điểm cực trị là
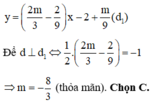
tìm m để đồ thị hàm số \(y=mx^4-4x^2+1\) có 3 điểm cực trị là đỉnh của một tam giác vuông cân
\(y'=4mx^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\mx^2=2\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A, B, C với \(\left\{{}\begin{matrix}A\left(0;1\right)\\B\left(\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\\C\left(-\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\end{matrix}\right.\)
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-\dfrac{4}{m}\right)\)
\(AH=\left|y_A-y_H\right|=\dfrac{4}{m}\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{\dfrac{2}{m}}\)
Tam giác ABC luôn cân tại A nên nó vuông cân khi \(AH=\dfrac{1}{2}BC\)
\(\Leftrightarrow\dfrac{4}{m}=\sqrt{\dfrac{2}{m}}\Rightarrow m=8\)
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Cho hàm số y = x^4 + 2(m + 1)x^2 + 1
a) Khảo sát và vẽ đồ thị khi m = 1
b) Tìm m để đồ thị hàm số có 3 điểm cực trị. Tìm phương trình đường cong đi qua các điểm cực trị đó
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 − 3 x 2 − m x + 2 có hai điểm cực trị A và B sao cho các điểm A, B và M(0;3) thẳng hàng.
A. m = -3
B. Không tồn tại m
C. m = − 2
D. m = 3
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )