Cho x thỏa mãn phương trình log 2 5.2 x − 8 2 x + 2 = 3 − x . Giá trị của biểu thức P = x log 2 4 x là:
A. P = 4
B. P = 8
C. P = 2
D. P = 1
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
Cho phương trình \(x^2-2\left(m+4\right)x+m^2-8=0\)
Tìm m để phương trình thỏa mãn \(x_1,x_2\) thỏa mãn:
\(A=x^2_1+x^2_2-x_1-x_2\) đạt giá trị nhỏ nhất.
\(B=x^2_1+x^2_2-x_1x_2\) đạt giá trị nhỏ nhất.
\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16
bài 1: cho phương trình \(x^2-2\left(m+2\right)x+m-3=0\)
Tìm m sao cho
a)phương trình có 2 nghiệm thỏa mãn \(\left(2x_1+1\right)\left(2x_2+1\right)=8\)
b)phương trình có 2 nghiệm thỏa mãn\(P=x_1^2+x_2^2-3x_1x_2\) nhỏ nhất
a)
Ta có: \(\Delta=\left[-2\left(m+2\right)\right]^2-4\cdot1\cdot\left(m-3\right)\)
\(=\left(-2m-4\right)^2-4\left(m-3\right)\)
\(=4m^2+16m+16\ge0\forall x\)
Suy ra: Phương trình \(x^2-2\left(m+2\right)x+m-3=0\) luôn có nghiệm với mọi m
Áp dụng hệ thức Viet, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+2\right)=2m+4\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(\left(2x_1+1\right)\left(2x_2+1\right)=8\)
\(\Leftrightarrow4\cdot x_1x_2+2\cdot\left(x_1+x_2\right)+1=8\)
\(\Leftrightarrow4\left(m-3\right)+2\left(2m+4\right)+1=8\)
\(\Leftrightarrow4m-12+4m+8+1=8\)
\(\Leftrightarrow8m=8+12-8-1\)
\(\Leftrightarrow8m=11\)
hay \(m=\dfrac{11}{8}\)
Tiếp tục với bài của bạn Nguyễn Lê Phước Thịnh
b)
Ta có: \(x_1^2+x_2^2-3x_1x_2=\left(x_1+x_2\right)^2-5x_1x_2\)
\(\Rightarrow P=4m^2+11m+31=4m^2+2\cdot m\cdot\dfrac{11}{2}+\dfrac{121}{4}+\dfrac{3}{4}\) \(=\left(2m+\dfrac{11}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu bằng xảy ra \(\Leftrightarrow2m+\dfrac{11}{2}=0\Leftrightarrow m=-\dfrac{11}{4}\)
Vậy \(P_{Min}=\dfrac{3}{4}\) khi \(m=-\dfrac{11}{4}\)
cho phương trình x^2-(m+2)x+m+8=0 , tìm m để phương trình có hai nghiệm phân biệt dương thỏa mãn x1^3-x2=0
Cho phương trình: \(x^2+2\left(m+1\right)x-8=0\left(1\right)\). Tìm \(m\) để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2=x_2\)
cái này tínhd đen ta r áp dụng hệ thức vi ét
cái biêủ thức đề bài biến đổi để kết hợp với pt tổng trong Viet ra hệ pt tìm ra x1 x2 ròi that vào pt tích trong viet
Cho phương trình: x²-2(m+1)x+m²+m=0
Tìm m để phương trình có nghiệm x1;x2 thỏa mãn điều kiện: 1/x1² + 1/x2² = 1/8
Ta có:
\(\text{∆}'=\left(m+1\right)^2-\left(m^2+m\right)\)
\(=m^2+2m+1-\left(m^2+m\right)=m+1\)
Để phương trình có 2 nghiệm phân biệt x1, x2
\(\Leftrightarrow\text{∆}'>0\Leftrightarrow m+1>0\Leftrightarrow m>-1\)
Áp dụng hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+m\end{matrix}\right.\)
Ta có: \(\dfrac{1}{x_1^2}+\dfrac{1}{x^2_2}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{x_1^2+x^2_2}{x_1^2.x_2^2}=\dfrac{1}{8}\)
\(\Leftrightarrow8[\left(x_1+x_2\right)^2-2x_1.x_2]=x_1^2.x_2^2\)
\(\Leftrightarrow8[[2\left(m+1\right)]^2-2\left(m^2+m\right)]=\left(m^2+m\right)^2\)
\(\Leftrightarrow8\left[4m^2+8m+4-2m^2-2m\right]=m^4+2m^3+m^2\)
\(\Leftrightarrow\)\(8\left[2m^2+6m+4\right]=m^4+2m^3+m^2\)
\(\Leftrightarrow m^4+2m^3-15m^2-48m-32=0\)
\(\Leftrightarrow\left(m+1\right)\left(m^3+m^2-16m-32\right)=0\)
Vì m>-1
\(\Leftrightarrow m^3+m^2-16m-32=0\)
Đến đây nghiêm xấu bạn xem lại đề hoặc có thể sử dụng CTN Cardano
Cho Phương trình x2 - 2x + m - 8. Tìm m để 2 nghiệm của phương trình thỏa mãn 3x1 - x2 = 0
theo đl VI-ET: X1 + X2 =2 VÀ X1.X2 = m -8.
giải hệ phương trình : 3x1 -x2 = 0 và x1 +x2 =2
ta tìm được x1 =1/2 và x2 =3/2
thay x1 , x2 vào x1.x2 = m-8
=> m =35/4
Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P = x 2 1 + 2 y + 4 y 2 1 + x là:
A. 6
B. 32 5
C. 31 5
D. 29 5
Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
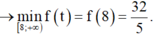
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .
Giải các phương trình sau:
a) \({\left( {\frac{1}{4}} \right)^{x - 2}} = \sqrt 8 \);
b) \({9^{2x - 1}} = {81.27^x}\);
c) \(2{\log _5}\left( {x - 2} \right) = {\log _5}9\);
d) \({\log _2}\left( {3{\rm{x}} + 1} \right) = 2 - {\log _2}\left( {x - 1} \right)\).
\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)
\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)
c, ĐK: \(x-2>0\Rightarrow x>2\)
\(2log_5\left(x-2\right)=log_59\\
\Leftrightarrow log_5\left(x-2\right)^2=log_59\\
\Leftrightarrow\left(x-2\right)^2=3^2\\
\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.
d, ĐK: \(x-1>0\Leftrightarrow x>1\)
\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)