Cho tứ diện MNPQ. Gọi I, J, K lần lượt là trung điểm các cạnh MN, MP, MQ. Tỉ số thể tích V M I J K V M N P Q bằng:
A. 1 4
B. 1 3
C. 1 8
D. 1 6
Cho tứ diện MNPQ. Gọi I;J;K lần lượt là trung điểm các cạnh MN;MP;MQ. Tỉ số thể tích V M I J K V M N P Q bằng
A. 1 4
B. 1 3
C. 1 8
D. 1 6
Cho tứ diện MNPQ. Gọi I ; J ; K lần lượt là trung điểm của các cạnh M N ; M P ; M Q . Tỉ số thể tích V M I J K V M N P Q bằng
A. 1 3
B. 1 4
C. 1 6
D. 1 8
Cho tứ diện NMPQ. Gọi I, J, K lần lượt là trung điểm của các cạnh MN, MP, MQ. Tỉ số thể tích V M I J K V M N P Q bằng:
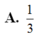

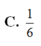
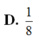
Cho tứ giác MNPQ. Gọi H, I, J, K lần lượt là trung điểm của MN, MP, PQ, QN. Tứ giác HKJI là hình gì? Vì sao? Tìm điều kiện để tứ giác MNPQ và tứ giác HKJI là hình thoi
Cho tứ giác MNPQ. Gọi H,I,J,K lần lượt là trung điểm của MN, MP,PQ,QN
a) Tứ giác HKJI là hình gì ? Vì sao
b) Tìm điều kiện để tứ giác MNPQ và tứ giác HKJI là hình thoi
a: Xét ΔMNP có
H là trung điểm của MN
I là trung điểm của MP
Do đó: HI là đường trung bình
=>HI//NP và HI=NP/2(1)
Xét ΔPQN có
J là trung điểm của PQ
K là trung điểm của QN
Do đó: JK là đường trung bình
=>JK//PN và JK=PN/2(2)
Từ (1) và (2) suy ra HI//KJ và HI=KJ
hay HKJI là hình bình hành
b: Để HKJI là hình thoi thì HJ⊥KI
hay MP⊥NQ
Cho tứ giác ABCD có: M; N; P; Q lần lượt là trung điểm của các cạnh AB; BC; CD; DA.
a) Chứng minh MN // PQ
b) Gọi I; K; H lần lượt là trung điểm của MQ; MP; NP. Chứng minh ba điểm I; K; H thẳng hàng
Bài này ko khó lắm đâu. Bạn chỉ cần nghĩ một chút thôi.
a,Nối A với C.
Xét tam giác BAC có: M là trung điểm của AB, N là trung điểm của BC
Suy ra: MN là đường trung bình của tam giác BAC
Nên MN song song với BC.(1)
Xét tam giác ACD có: P là trung điểm của CD và Q là trung điểm của AD.
Do đó: PQ là đường trung bình của tam giác ACD
Nên PQ song song với BC. (2)
Từ (1) và (2), ta có: MN song song với PQ.
b, Xét tam giác MQP có: I là trung điểm của MQ, K là trung điểm của MP
Vì thế IK là đường trung bình của tam giác MQP
Suy ra: IK song song với PQ.
Tương tự, KH là đường trung bình của tam giác MNP
Nên KH song song với MN.
Mà MN song song với PQ
Do đó: KH song song với PQ
Qua điểm K nằm ngoài đường thẳng PQ, có 2 đường thẳng IK,KH cùng song song với PQ nên theo tiên đề Ơclít , 3 điểm I,K,H thẳng hàng.
Chúc bạn học tốt.
Cho tứ diện ABCD. Gọi M; N; P lần lượt là các điểm thuộc cạnh AB; AC; BD; M N ∩ B C = I ; M P ∩ A D = J ; N J ∩ I P = K . Tìm mệnh đề đúng:
A. C; D; I thẳng hàng
B. C; M; K thẳng hàng
C. C; D; K thẳng hàng
D. M; I; J thẳng hàng
cho tứ giác abcd. gọi m, n, p, q lần lượt là trung điểm của các cạnh ab, bc, cd, da và i, k là trung điểm các đường chéo ac, bd. chứng minh rằng:
a) tứ giác mnpq, inkq là hình bình hành.
b) gọi o là giao điểm của mp, nq. chứng minh 3 điểm i, o, k thẳng hàng
các bạn giúp mình với ạ, mình cảm ơn rất nhiều!
a) Ta có:-
- M là trung điểm của AB
⇒ AM = MB.
- N là trung điểm của BC
⇒ BN = NC.
- P là trung điểm của CD
⇒ CP = PD.
- Q là trung điểm của DA
⇒ DQ = QA.
Do đó, ta có: AM = MB = BN = NC = CP = PD = DQ = QA.
⇒ tứ giác MNPQ là hình bình hành.
Có:
- I là trung điểm của AC
⇒AI = IC.
- K là trung điểm của BD
⇒ BK = KD.
Do đó, ta có: AI = IC = BK = KD.
⇒ tứ giác INKQ là hình bình hành.
b)Gọi O là giao điểm của MP và NQ ta có:
MP // AB và NQ//CD ( M và N là trung điểm của AB và CD).
⇒ MP song song với NQ.
do đó :O nằm trên MP và NQ.
Gọi H là giao điểm của MI và NK ta có:
MI // AC và NK // BD (do I và K là trung điểm của đường chéo AC và BD).
⇒ MI song song với NK.
Do đó: H nằm trên cả MI và NK.
Gọi G là giao điểm của OH và BD ta có:
OH //MP và BD // MP (do O nằm trên MP và NQ, và H nằm trên MI và NK).
⇒ OH song song với BD.
doo đó: G nằm trên OH và BD.
⇒ I, O, K thẳng hàng.(ĐPCM)
a: Xét ΔBAC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔDAC có DQ/DA=DP/DC
nên PQ//AC và PQ/AC=DQ/DA=1/2
=>PQ=1/2AC
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔCAB có CI/CA=CN/CB=1/2
nên IN//AB và IN=1/2AB
Xét ΔDAB có DQ/DA=DK/DB=1/2
nên QK//AB và QK=1/2AB
=>IN//QK và IN=QK
=>INKQ là hình bình hành
b: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm của NQ
INKQ là hbh
=>IK cắt NQ tại trung điểm của mỗi đường
=>I,O,K thẳng hàng
1.cho khối lăng trụ tam giác ABC.A'B'C'. Gọi I,J,K lần lượt là trung điểm của AB,AA',B'C' . Mặt phẳng (IJK) chia khối lăng trụ thành 2 phần.Tính tỉ số thể tích của 2 phần đó.
2.Cho khối tứ diện ABCD có cạnh AB>1,các cạnh còn lại có độ dài không lớn hơn 1. Gọi V là thể tích của khối tứ diện. Tìm giá trị lớn nhất của V.
Cho Hình Chữ NHật MNPQ. Hai đường chéo MP và NQ cắt nhau tại O . Trên đoạn ON lấy điểm E . Lấy điểm F sao cho E là trung điểm của đoạn PF .
a) Cho MN =6 cm; MP =10 cm . Tính diện tích hcn MNPQ
b) c/m tứ giác MFNQ là hình thang
c)Gọi I, K là chân đường vuông góc kẻ từ F đến đoạn thẳng MQ , MN . C/m ba điểm I,K,E tẳng hàng