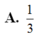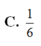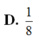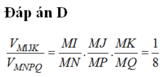Các câu hỏi tương tự
Cho tứ diện MNPQ. Gọi I, J, K lần lượt là trung điểm các cạnh MN, MP, MQ. Tỉ số thể tích
V
M
I
J
K
V
M
N
P
Q
bằng: A.
1
4...
Đọc tiếp
Cho tứ diện MNPQ. Gọi I, J, K lần lượt là trung điểm các cạnh MN, MP, MQ. Tỉ số thể tích V M I J K V M N P Q bằng:
A. 1 4
B. 1 3
C. 1 8
D. 1 6
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp
α
qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của
α
với BD và AD. Xét các mệnh đề sau: (1) MP // BC (2) MQ // AC (3) PQ // AI (4) (MPQ) // (ABC) Số mệnh đề đúng là:
Đọc tiếp
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của α với BD và AD. Xét các mệnh đề sau:
(1) MP // BC
(2) MQ // AC
(3) PQ // AI
(4) (MPQ) // (ABC)
Số mệnh đề đúng là:
![]()
![]()
![]()
Cho khối lăng trụ tam giác ABC.ABC có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA và BB. Khi đó thể tích của khối đa diện ABCIJC bằng.
Đọc tiếp
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng.
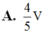
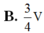
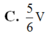
Cho khối lăng trụ tam giác ABC.ABC có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA và BB. Khi đó thể tích của khối đa diện ABCIJC bằng.
Đọc tiếp
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng.
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng: A.
5
24
V B.
1
4
V C.
7
24
V D.
1
3
V
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng:
A. 5 24 V
B. 1 4 V
C. 7 24 V
D. 1 3 V
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số
V
V
có giá trị nhỏ nhất bằng A.
1
5
B.
3
8
C.
1
3
D.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5
B. 3 8
C. 1 3
D. 1 2
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng: A.
1
2
B.
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng:
A. 1 2
B. 2 3
C. 1 3
D. 3 8
Cho khối chóp S.ABC có thể tích bằng 16
c
m
3
. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC. Tính thể tích V của khối tứ diện AMNP. A.
V
8
c
m
3
B.
V
14
c...
Đọc tiếp
Cho khối chóp S.ABC có thể tích bằng 16 c m 3 . Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC. Tính thể tích V của khối tứ diện AMNP.
A. V = 8 c m 3
B. V = 14 c m 3
C. V = 12 c m 3
D. V = 2 c m 3
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy
I
∈
A
C
,
J
∈
D
N
sao cho IJ // BM. Độ dài IJ theo a là: A.
a
3
3
B....
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là:
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2