Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5 là đường thẳng:
A. Có hệ số góc dương.
B. Có hệ số góc âm.
C. Song song với trục hoành.
D. Song song với đường thẳng y = - 5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tiếp tuyến của đồ thị hàm số y = x 4 - 3 x 2 + 1 tại điểm cực tiểu của đồ thị có phương trình
A. y = - 5 4 x
B. y = - 5 4
C. y = 5 4 x
D. y = - 5 4
Đáp án B
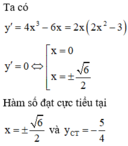
Vậy tiếp tuyến của đồ thị hàm số tại điểm cực tiểu có phương trình y = - 5 4
Cho hàm số y = f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu bằng – 3 tại điểm x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x= -3
A. f'(-3)= 0
B. f'(-3)= 2
C. f'(-3)= 1
D. f'(-3)= -2
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 − 2 x 2 + 3 x − 5
A. Có hệ số góc dương
B. Song song với trục hoành
C. Có hệ số góc bằng -1
D. Song song với đường thẳng x = 1
Phương pháp:
+) Xác định điểm cực tiểu của đồ thị hàm số.
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu vừa tìm được và kết luận
Cách giải:

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5
A. song song với đường thẳng x = 1
B. song song với trục hoành
C. có hệ số góc dương
D. có hệ số góc bằng -1
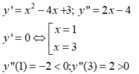
Do đó, hàm số đã cho đạt cực tiểu tại điểm x = 3 => y = -5
Phương trình tiếp tuyến tại điểm cực tiểu là:
y = 0(x - 3) – 5 = -5
Đây là đường thẳng song song với trục hoành,
Chọn B.
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5 là đường thẳng
A. song song với đường thẳng x = 1
B. song song với trục hoành
C. có hệ số góc dương.
D. có hệ số góc bằng -1
Đáp án B.
Ta có: y’ = x2 – 4x + 3;
y' = 0 ó x= 3 hoặc x= 1
Bảng biến thiên:
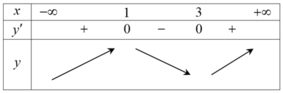
Hàm số đạt cực tiểu tại điểm M(3;-5).
y'(3) = 0;
Phương trình tiếp tuyến là: y = 0(x – 3) – 5 ó y = -5
Đường thẳng này song song với trục hoành.
cho hàm số y = x 3 − 3 x 2 2 , có đồ thị là (c). gọi m là một điểm thuộc đồ thị (c). viết phương trình tiếp tuyến của ( c) tại m, biết m cùng với hai điểm cực trị của đồ thị tạo thành một tam giác có diện tích bằng 6
Viết phương trình tiếp tuyến của đồ thị hàm số y = - x 4 + 6 x 2 - 5 tại điểm cực tiểu của nó
A. y = 5
B. Y = - 5
C. y = 0
D. y = x + 5
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )