Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho đồ thị hàm số C : y = − 2 x + 3 x − 1 . Viết phương trình tiếp tuyến của đồ thị (C) tại
giao điểm của (C) và đường thẳng y = x − 3 .
A. y = − x + 3 v à y = − x − 1
B. y = − x − 3 v à y = − x + 1
C. y = x − 3 v à y = x + 1
D. y = − x + 3 v à y = − x + 1
Đáp án B
Tọa độ giao điểm của (C) và đường thẳng y = x − 3 là nghiệm của hệ:
y = − 2 x + 3 x − 1 y = x − 3 ⇔ x = 2 y = − 1 x = 0 y = − 3 ⇒ A ( 2 ; − 1 ) B ( 0 ; − 3 )
y ' = − 1 x − 1 2
Phương trình tiếp tuyến với ( C) tại A ( 2 ; − 1 ) là:
y = − 1 2 − 1 2 ( x − 2 ) − 1 = − x + 1
Phương trình tiếp tuyến với ( C) tại B ( 0 ; − 3 ) là:
y = − 1 0 − 1 2 ( x − 0 ) − 3 = − x − 3
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Cho hàm số \(y=x^3-3x^2+2x\) có đồ thị (C)
a. Viết phương trình tiếp tuyến (C) tại điểm có hoành độ bằng -1
b. Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 6
c. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)
Cho hàm số y = 2 2 - x
Tìm giao điểm của (C ) và đồ thị hàm số y= x 2 +1 . Viết phương trình tiếp tuyến của (C ) tại mỗi giao điểm.
Phương trình hoành độ giao điểm của hai đường cong :
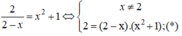
Phương trình (*) tương đương : 2 = 2x2 + 2 – x3 – x
⇔ x3 – 2x2 + x = 0 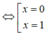 ( đều thỏa mãn khác 2).
( đều thỏa mãn khác 2).
Vậy tọa độ giao điểm của hai đường cong là A(0 ; 1) và B(1 ; 2)
+ Phương trình tiếp tuyến tại A là
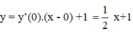
+ Phương trình tiếp tuyến tại điểm B(1 ; 2) là :
y = y’(1). (x – 1) + 2 = 2(x – 1)+ 2
Hay y = 2x
Cho hàm số y = x + 2 x + 1 có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị (C) với trục tung là
A. y = x – 2
B. y = –x + 2
C. y = –x + 1
D. y = –x –2
Viết phương trình tiếp tuyến của đồ thị hàm số:
\(y=\dfrac{-x+2}{x+1}\)
a, Tại giao điểm của đồ thị vs trục hoành
b, Tại giao điểm của đồ thị vs trục tung
c, Hệ số góc \(k=-3\)
Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm
Ta có: y' \(=\dfrac{-3}{\left(x+1\right)^2}\)
k=f'\(\left(x_0\right)\)\(\Rightarrow-3=\dfrac{-3}{\left(x_0+1\right)^2}\Leftrightarrow\left(x_0+1\right)^2=1\)\(\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-2\end{matrix}\right.\)
Với \(x_0=0\) ta có pt tiếp tuyến:
\(d:3x+y-2=0\)
Với \(x_0=-2\) ta có pt tiếp tuyến:
\(d:3x+y+10=0\)
a: Tọa độ giao điểm của (d) với trục Ox là:
y=0 và (-x+2)=0
=>x=2 và y=0
\(y'=\dfrac{\left(-x+2\right)'\left(x+1\right)-\left(-x+2\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{\left(-\left(x+1\right)+x-2\right)}{\left(x+1\right)^2}=\dfrac{-3}{\left(x+1\right)^2}\)
Khi x=2 thì y'=-3/(2+1)^2=-3/9=-1/3
y-f(x0)=f'(x0)(x-x0)
=>y-0=-1/3(x-2)
=>y=-1/3x+2/3
b: Tọa độ giao của (d) với trục Oy là;
x=0 và y=(-0+2)/(0+1)=2
Khi x=0 thì \(y'=\dfrac{-3}{\left(0+1\right)^2}=-3\)
y-f(x0)=f'(x0)(x-x0)
=>y-2=-3(x-0)
=>y=-3x+2
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
Cho hàm số y=x lnx có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với đường thẳng d:x-1=0 là
A.x-y+1=0
B.x+y-1=0
C.x-y=0
D.x-y-1=0
Cho hàm số y = x 3 - 3 x 2 + 3 có đồ thị là (C). Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x=1
A. y=2x-1
B. y=-x+2
C. y=-3x+3
D. y=-3x+4
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)