Cho x > 0 , x ≠ 1 thỏa mãn biểu thức 1 log 2 x + 1 log 3 x + . .. + 1 log 1993 x = M . Chọn khẳng định đúng trong các khẳng định sau
A. x = 1993 ! M 1993
B. x = 1993 ! M
C. x = 1993 M
D. x = 1993 ! M
Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P = x 2 1 + 2 y + 4 y 2 1 + x là:
A. 6
B. 32 5
C. 31 5
D. 29 5
Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
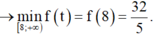
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .
Cho x, y > 0 thỏa mãn log x + 2 y = log x + log y . Khi đó, giá trị nhỏ nhất của biểu thức P = x 2 1 + 2 y + 4 y 2 1 + x
A. 6
B. 31 5
C. 32 5
D. 39 5
Cho x; y> 0 thỏa mãn log 2x+ log2y=log4(x+y) Tìm x; y để biểu thức P= x2+y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x=y=1
D. y = 2 3 ; x = 2 2 3
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà ![]()
Ta có
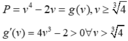
nên minP=
2
4
3
khi 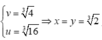
Chọn A.
Cho x, y >0 thỏa mãn log(x+2y)=logx+logy. Khi đó giá trị nhỏ nhất của biểu thức P = x 2 1 + 2 y + 4 y 2 1 + x là
A. 6.
B. 32/5
C. 31/5
D. 29/5
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
cho x>0 thỏa mãn X^2+1/X^2=14.Tính giá trị của biểu thức x^5+1/x^5
Cho biểu thức P=2x^2-1/x^2+x - x-1/x + 3/x+1
a,Rút gọn P
b,Tìm x để P=0
c,Tính giá trị của biểu thức P khi thỏa mãn x^2-x=0
a: \(P=\dfrac{2x^2-1-x^2+1+3x}{x\left(x+1\right)}=\dfrac{x^2+3x}{x\left(x+1\right)}=\dfrac{x+3}{x+1}\)
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số