Cho phân thức
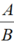
viết phân thức nghịch đảo của nó.
PB
Những câu hỏi liên quan
Cho phân thức \(\dfrac{A}{B}\) khác 0, viết phân thức nghịch đảo của nó ?
Với \(\dfrac{A}{B}\ne0\)
\(\Rightarrow\) Phân thức nghịch đảo là: \(\dfrac{B}{A}\)
Đúng 0
Bình luận (0)
Tìm phân thức nghịch đảo của mỗi phân thức sau:
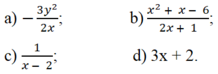
phân thức nghịch đảo của phân thức x-1/x+2
Phân thức nghịch đảo của \(\dfrac{x-1}{x+2}\) là \(\dfrac{x+2}{x-1}\)
Đúng 0
Bình luận (0)
phân thức nghịch đảo của phân thức 3x^2/x-1
Nghịch đảo của phân thức
(
x
-
2
y
)
/
(
x
-
y
)
là phân thức: A.
x
-
y
x
-
2
y
B.
2
y
-
x
y
-...
Đọc tiếp
Nghịch đảo của phân thức ( x - 2 y ) / ( x - y ) là phân thức:
A. x - y x - 2 y
B. 2 y - x y - x
C. x + 2 y x + y
D. 2 y - x x - y
Phân thức nghịch đảo của phân thức
x
x
+
2
với x ≠ 0; x ≠ -2 là: A.
x
x
+
2
B.
x
+
2
x
C.
−
x
+
2
x
D. ...
Đọc tiếp
Phân thức nghịch đảo của phân thức x x + 2 với x ≠ 0; x ≠ -2 là:
A. x x + 2
B. x + 2 x
C. − x + 2 x
D. − x x + 2
Tìm phân thức nghịch đảo của các phân thức sau: x + 1 x - 2 , 2 x 1 , x - 1
Hướng dẫn:
+ Phân thức nghịch đảo của phân thức (x + 1)/(x - 2) là (x - 2)/(x + 1).
+ Phân thức nghịch đảo của phân thức (2x)/1 là 1/(2x).
+ Phân thức nghịch đảo của phân thức x - 1 là 1/(x - 1).
Đúng 0
Bình luận (0)
a)Chứng minh rằng tổng của một phân số dương với nghịch đảo của nó không nhỏ hơn 2.
b) Tìm các phân số có tử và mẫu đều dương sao cho tổng của phân số đó với nghịch đảo của nó có giá trị nhỏ nhất.
a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.
Đúng 0
Bình luận (0)
Chứng minh rằng tổng của một phân số dương vơi số nghịch đảo của nó thì không nhỏ hơn 2
Viết số nghịch đaoả của -2 dưới dạng tổng các nghịch đảo của ba số nguyên khác nhau