Cho ba số phức a,b,c phân biệt, khác 0 và thỏa mãn a = b = c . Biết một nghiệm của phương trình a z 2 + bz + c = 0 có môđun bằng 1. Mệnh đề nào sau đây là đúng?
A. b 2 = 4ac
B. b 2 = ac
C. b 2 = 2ac
D. b 2 = 3ac
Cho a, b là các số thực thỏa mãn a > 0 v à a ≠ 1 biết phương trình a x - 1 a x = 2 c o s ( b x ) có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình a 2 x - 2 a x ( c o s b x + 2 ) + 1 = 0
A. 14
B. 0
C. 7
D. 28
Cho a,b,c là 3 số phức phân biệt khác 0 và modul của chúng bằng nhau .Nếu một nghiệm của phương trình az2 + bz + c = 0 có môđun bằng 1 thì khẳng định nào sau đây đúng.
A. c2 = ab
B. a2 = bc
C. b = ac
D. b2 = ac
Chọn D.
Giả sử z1; z2 là nghiệm của phương trình đã cho với |z| = 1.
Theo định lý Viet ta có 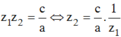 .Suy ra
.Suy ra 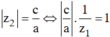
Bởi vì 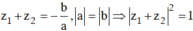 , suy ra
, suy ra ![]()
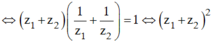
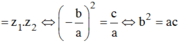
Cho các số thực a,b,c thỏa mãn 4a+b>8+2b và a+b+c<-1. Khi đó số nghiệm thực phân biệt của phương trình x 3 + a x 2 + b x + c = 0 bằng
A.0
B.3
C.2
D.1
Cho các số thực a,b,c thỏa mãn a+c>b+1 và 4a+2b+c<-8. Khi đó số nghiệm thực phân biệt của phương trình x 3 + a x 2 + b x + c = 0 bằng
A.0
B.3
C.2
D.1
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
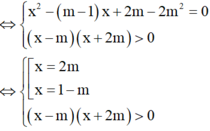
Điều kiện để pt đã cho có 2 nghiệm
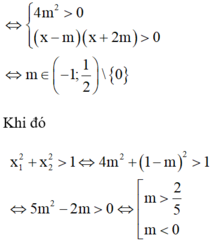
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2
Cho phương trình
2
log
4
2
x
2
−
x
+
2
m
−
4
m
2
+
log
1
2
x
2
+
m
x
−
2
m
2
=
0
Biết
S
=
a
;
b
∪
c
;
d
,
a
<
b
<
c
<
d
là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn
x
1
2
+
x
2
2
>
1
. Tính giá trị biểu thức
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Cho a, b, c ∈R,a ≠ 0, z 1 , z 2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình a x 2 +bx+c=0. Hãy tính z 1 + z 2 và z 1 . z 2 theo hệ số a, b, c.
Cách 1 :
Phương trình a z 2 + bz + c = 0 có Δ = b 2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức 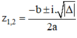
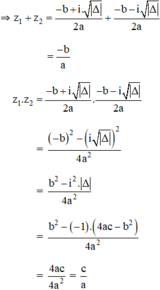
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
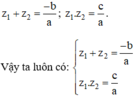
Cách 2 :

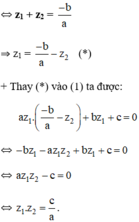
Cho các số thực a,b,c thỏa mãn 4a+b>8+2b và a+b+c<-1. Khi đó phương trình x^3 + ax^2 + b^x + c = 0 có bao nhiêu nghiệm thực phân biệt?
giúp em với ạ
thôi để giải luôn
Xét phương trình: \(x^3+ax^2+bx+c=0\left(1\right)\)
Đặt : \(f\left(x\right)=x^3+2x^2+bc+c\)
Từ giả thiết \(\left\{{}\begin{matrix}4a+c>8+2b\Rightarrow-8+4a-2b+c>0\Rightarrow f\left(-2\right)>0\\a+b+c< -1\Rightarrow1+a+b+c< 0\Rightarrow f\left(1\right)< 0\end{matrix}\right.\)
Do đó \(f\left(-2\right).f\left(1\right)< 0\) nên pt (1) có ít nhất một nghiệm trong \(\left(-2;1\right)\)
Ta nhận thấy:
\(\overset{lim}{x\rightarrow-\infty}f\left(x\right)=-\infty\) mà \(f\left(-2\right)>0\) nên phương trình (1) có ít nhất một nghiệm \(\alpha\in\left(-\infty;-2\right)\)
Tương tự: \(\overset{lim}{x\rightarrow+\infty}f\left(x\right)=+\infty\) mà \(f\left(1\right)< 0\) nên phương trình (1) có ít nhất một nghiệm \(\beta\in\left(1+\infty\right)\)
Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm nên pt trên sẽ có 3 nghiệm thực phân biệt.
Xét các số nguyên dương a,b sao cho phương trình b ln 2 x + a ln x + 3 = 0 có hai nghiệm phân biệt x 1 , x 2 và phương trình 3 log 2 x + a log x + b = 0 có hai nghiệm phân biệt x 3 , x 4 thỏa mãn ln x 1 x 2 10 > log x 3 x 4 6 Tính giá trị nhỏ nhất của S=5a + 3b
A. 102
B. 101
C. 96
D. 99