Cho N=9 9... 9 4 0 0 ... 0 9
Tính \(\sqrt{N}\)
Help
Cho hai biểu thức \(A=\dfrac{7}{\sqrt{x+8}}\)và \(B=\dfrac{\sqrt{x}}{\sqrt{x-3}}+\dfrac{2\sqrt{x-24}}{x-9}\)với x > 0 ; x khác 9
Tính giá trị của A khi x = 16
Cho N =\(99...9400...09\). Tính \(\sqrt{N}\)( Tại mình không biết ngoặc ở đưới mỗi số để chỉ ra chư số, mình viết ra như này ạ: Từ số 99...9( 10 chữ số 9), số 4 đứng một mình, bắt đầu từ số 0 đứng sau số 4 cho đến số 0 đứng trước số 9 là 10 chữ số 0), 9 giữ nguyên )
* Về phần lời giải mình chưa hiểu như sau:
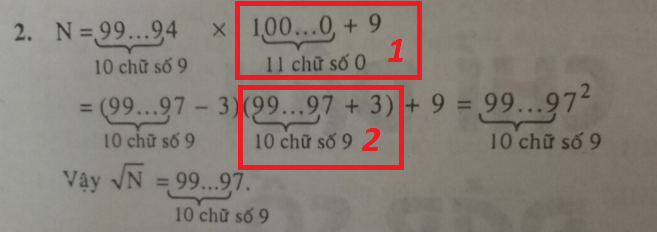
* Phần lười giải này các bạn chỉ cho mình: 2 cái mình đánh dấu số 1 và 2 và khoanh đỏ.
* kHOANH ĐỎ SỐ 1: Tại sao lúc đầu đề cho chỉ có 10 chữ số 0 thôi nhưng khi tách ra như lời giải lại là 11 chữ số 0. ( chi tiets giúp mình nhá)
* KHOANH ĐỎ SỐ 2: Từ chỗ này làm sao để nghĩ và làm nhanh được để đưa nó về khung khoanh tròn đỏ số 1 ạ. ( dùng cách như nào ạ )
\(\underbrace{999....9}_{10} 4\underbrace{000..0}_{10}9=\underbrace{999....9}_{10} 4\underbrace{00...0}_{11}+9\)
\(=\underbrace{999....9}_{10}4\times 1\underbrace{00...0}_{11}+9\)
\(=(\underbrace{999....9}_{10}7-3)\times (\underbrace{99....9}_{10}7+3)-9\)
(em tưởng tượng 1000 có 3 chữ số 0 đằng sau, biểu diễn được thành 997+3 có 3-1=2 chữ số 9)
Tất cả những vấn đề em hỏi đều thuộc lý thuyết phân tích cấu tạo số cơ bản. Tất nhiên, lời giải sẽ có 1 chút tắt (không đáng kể).
Tip: Em chịu khó viết ra nháp từng bước một và đọc kỹ. Nếu thấy số dài mà không hiểu vì sao người ta làm vậy, em thử với bộ số nhỏ hơn có phong cách tương tự (ví dụ 994009)
Cho N = 99.....99(10 chữ số 9) 4 00....0(mười chữ số 0) 9.Tính can N
A=\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)(x≥0,x≠4,x≠9)
1,Tìm x để A.\(\sqrt{x}\)=-1
2,Tìm x∈ Z để A∈Z
3, Tìm Min \(\dfrac{1}{A}\)
4,Tìm x∈N để A là số nguyên dương lớn nhất
5,Khi A+\(|A|\)=0, tìm GTLN của bth A.\(\sqrt{x}\)
1: Ta có: \(A=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
Để \(A=-\dfrac{1}{\sqrt{x}}\) thì \(x+\sqrt{x}=-\sqrt{x}+3\)
\(\Leftrightarrow x+2\sqrt{x}-3=0\)
\(\Leftrightarrow\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow x=1\left(nhận\right)\)
2: Để A nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-1;1;2;-2;4;-4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{2;4;5;1;7\right\}\)
\(\Leftrightarrow x\in\left\{16;25;1;49\right\}\)
tìm \(limu_n=L>0\) thì \(lim\sqrt{\dfrac{n\left(u_n+9\right)}{n+5}}\)=?
Lời giải:\(\lim\limits\sqrt{\frac{n(u_n+9)}{n+5}}=\lim\limits\sqrt{\frac{u_n+9}{1+\frac{5}{n}}}=\lim\limits\sqrt{u_n+9}=\sqrt{L+9}\)
1/Mỗi số sau là bình phương của số tự nhiên nào?
a. A = 99...9 00...0 25 (có n chữ số 9 và n chữ số 0)
b. B = 99...9 8 00..0 1 (có n chữ số 9 và n chữ số 0)
c. C = 44...4 88...8 9 (có n chữ số 4 và n - 1 chữ số 8)
d. D = 11..1 22...2 5 (có n chữ số 1 và n + 1 chữ số 2)

B = 99..9 (n số 9 )
= 99...900...0 ( n+1 số 9 và n+1 số 0).
Đặt x =11...1 (n+1 số 1) .
Thì B =9x.10^(n+1) -9x =9x.[10^(n+1) -1] =9x.99...9 (n+1 số 9 )
nên B = 9x.9x = (9x)^2 =(99...9)^2 (n+1 số 9 ).
Chứng minh 224 99...9 1 00...0 9 là số chính phương với 99...9 là n-2 số 9 va 00...0 là n số 0
Mỗi số sau đây là bình phương của số tự nhiên nào ?
a) A= 999...9000...0 25
( n số 9) ( n số 0 )
b) B= 99...9 8 00...0 1
( n số 9 ) ( n số 0 )
c) C= 44...488...8 9
( n số 4 ) ( n-1 số 8 )
d) D = 11...1 22...2 5
( n số 1) ( n+1 số 2 )
Ta có :
x=99....90....025=99....90....025
| n số 9 ||n số 0|
Dễ thấy 10^n-1=999...910n−1=999...9( n chữ số 9 )
Ví dụ 10-1=910−1=9
10000-1=999910000−1=9999
......
\Rightarrow\left(10^n-1\right).10^{n+2}+25⇒(10n−1).10n+2+25
=10^n.10^{n+2}-10^{n+2}+25=10n.10n+2−10n+2+25
=10^{2n+2}-10.10^{n+1}+25=102n+2−10.10n+1+25
=\left(10^{n+1}\right)^2-2.5.10^{n+1}+5^2=(10n+1)2−2.5.10n+1+52
=\left(10^{n+1}-5\right)^2=(10n+1−5)2 là số chính phương.
Vậy ...
a\(\sqrt{x-1}+2\sqrt{9x-9}-14=0\)
b,\(\sqrt{2-x}-\sqrt{4-x^2}=0\)
\(a,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}+6\sqrt{x-1}=14\\ \Leftrightarrow7\sqrt{x-1}=14\\ \Leftrightarrow\sqrt{x-1}=2\Leftrightarrow x-1=4\\ \Leftrightarrow x=5\left(tm\right)\\ b,ĐK:-2\le x\le2\\ PT\Leftrightarrow\sqrt{2-x}\left(1-\sqrt{2+x}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2-x=0\\2+x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
a) ĐKXĐ: \(x\ge1\)
\(pt\Leftrightarrow\sqrt{x-1}+6\sqrt{x-1}=14\)
\(\Leftrightarrow7\sqrt{x-1}=14\Leftrightarrow\sqrt{x-1}=2\)
\(\Leftrightarrow x-1=4\Leftrightarrow x=5\left(tm\right)\)
b) ĐKXĐ: \(-2\le x\le2\)
\(pt\Leftrightarrow\sqrt{2-x}-\sqrt{\left(2-x\right)\left(x+2\right)}=0\)
\(\Leftrightarrow\sqrt{2-x}\left(1-\sqrt{x+2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2-x=0\\x+2=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)