Với a là số thực dương khác 1, giá trị biểu thức l o g a a a bằng
A. 2/3.
B. 4/3.
C. 3/2.
D. 3/4
Cho a, b, c là các số thực dương khác 1 thỏa log a 2 b + log b 2 c = log a c d - 2 log b c b - 3 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = log a b - log b c . Giá trị của biểu thức S =2m+3M bằng
A. S=1/3.
B. S =2/3.
C. S =2.
D. S =3.
Cho a, b, c là các số thực dương khác 1 thỏa log a 2 b + log b 2 c = log a c b - 2 log b c b - 3
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = log a b - log b c Giá trị của biểu thức S = 2 m + 3 M bằng
A. S = 1 3
B. S = 2 3
C. S = 2
D. S = 3
Đặt 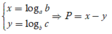 và giả thiết trở thành
và giả thiết trở thành
![]()
Suy ra ![]()
![]()
Phương trình có nghiệm khi ![]()
Chọn D.
Cho số thực \(a > 0\).
a) Hai biểu thức \(\sqrt[6]{{{a^4}}}\) và \(\sqrt[3]{{{a^2}}}\) có giá trị bằng nhau không? Giải thích.
b) Chỉ ra ít nhất hai biểu thức khác nhau có giá trị bằng \(\sqrt[3]{{{a^2}}}\).
a, Ta có: \(\sqrt[6]{a^4}=\sqrt[3]{\sqrt{a^4}}=\sqrt[3]{\sqrt{\left(a^2\right)^2}}=\sqrt[3]{\left|a^2\right|}=\sqrt[3]{a^2}\)
Vậy \(\sqrt[6]{a^4}=\sqrt[3]{a^2}\)
b, \(\sqrt[3]{a^2}=\sqrt[9]{a^6}=\sqrt[12]{a^8}\)
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
Cho ba số thực dương a, b, c thoả mãn :a2+b2+c2=3 . Tìm giá trị nhỏ nhất của biểu thức:
\(M=\dfrac{a^5}{b^3+c^2}+\dfrac{b^5}{c^3+a^2}+\dfrac{c^5}{a^3+b^2}+a^4+b^4+c^4\)
\(\dfrac{a^5}{b^3+c^2}+\dfrac{b^3+c^2}{4}+\dfrac{a^4}{2}\ge3\sqrt[3]{\dfrac{a^9.\left(b^3+c^2\right)}{8\left(b^3+c^2\right)}}=\dfrac{3a^3}{2}\)
Tương tự và cộng lại:
\(\Rightarrow M-\dfrac{a^4+b^4+c^4}{2}+\dfrac{a^3+b^3+c^3}{4}+\dfrac{a^2+b^2+c^2}{4}\ge\dfrac{3}{2}\left(a^3+b^3+c^3\right)\)
\(\Rightarrow M\ge\dfrac{a^4+b^4+c^4}{2}+\dfrac{5}{4}\left(a^3+b^3+c^3\right)-\dfrac{3}{4}\)
Mặt khác ta có:
\(\dfrac{1}{2}\left(a^4+b^4+c^4\right)\ge\dfrac{1}{6}\left(a^2+b^2+c^2\right)^2=\dfrac{3}{2}\)
\(\left(a^3+a^3+1\right)+\left(b^3+b^3+1\right)+\left(c^3+c^3+1\right)\ge3\left(a^2+b^2+c^2\right)=9\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge9\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow M\ge\dfrac{3}{2}+\dfrac{15}{4}-\dfrac{3}{4}=...\)
Cho log a b = 2 , với a, b là các số thực dương và 1 khác 1. Tính giá trị biểu thức T = log a 2 b 6 + log a b
A. T = 8
B. T = 7
C. T = 5
D. T = 6
a. Tìm giá trị của $x$ sao cho biểu thức $A = x - 1$ có giá trị dương.
b. Đưa thừa số ra ngoài dấu căn, tính giá trị biểu thức $B = 2\sqrt{2^2.5} - 3\sqrt{3^2.5} + 4\sqrt{4^2.5}$.
c. Rút gọn biểu thức $C = \left(\dfrac{1-a\sqrt a}{1-\sqrt a} + \sqrt a\right) \left(\dfrac{1-\sqrt a}{1-a}\right)^2 $ với $a \ge 0$ và $a \ne 1$.
a, Để A nhận giá trị dương thì \(A>0\)hay \(x-1>0\Leftrightarrow x>1\)
b, \(B=2\sqrt{2^2.5}-3\sqrt{3^2.5}+4\sqrt{4^2.5}\)
\(=4\sqrt{5}-9\sqrt{5}+16\sqrt{5}=\left(4-9+16\right)\sqrt{5}=11\sqrt{5}\)
( theo công thức \(A\sqrt{B}=\sqrt{A^2B}\))
c, Với \(a\ge0;a\ne1\)
\(C=\left(\frac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\frac{1-\sqrt{a}}{1-a}\right)^2\)
\(=\left(\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\left(\frac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(\sqrt{a}+1\right)^2.\frac{1}{\left(\sqrt{a}+1\right)^2}=1\)
Cho các số thực a;b;c khác 0 thỏa mãn a^3+b^3+c^3=3abc. Tính giá trị biểu thức A=(1+a/b)(1+b/c)(1+c/a)
a^3+b^3+c^3=3abc
=>(a+b)^3+c^3-3ab(a+b)-3bac=0
=>(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)=0
=>(a+b+c)(a^2+b^2+c^2-ab-ac-bc)=0
=>a^2+b^2+c^2-ab-bc-ac=0
=>2a^2+2b^2+2c^2-2ab-2bc-2ac=0
=>(a-c)^2+(a-b)^2+(b-c)^2=0
=>a=b=c
=>A=(1+b/b)(1+b/b)(1+c/c)
=2*2*2=8
Cho a,b,c là 3 số thực dương thỏa mãn a+b+c=3.Tìm giá trị nhỏ nhất của biểu thức \(M=\frac{a+1}{1+b^2}+\frac{b+1}{1+c^2}+\frac{c+1}{1+a^2}\)