Tìm tổng các giá trị nguyên của tham số m để hàm số y = m x 4 + m 2 - 25 x 2 + 2 có một điểm cực đại và hai điểm cực tiểu.
A. 10
B. -10
C. 0
D. 15
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
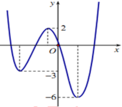
A. 12
B. 15
C. 18
D. 9
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
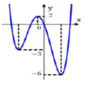
A. 9
B. 7
C. 12
D. 18
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số sau: y = f(x) = ( x2 - 2( m + 4) x + 2m + 12).ex. Tìm tổng các giá trị nguyên của m để hàm số nghịch biến trên TXĐ là S thì giá trị của S sẽ là:
A. 15
B. -12
C. -15
D. -10
Chọn C.
+) TXĐ: D = R
+) Ta có đạo hàm y’ = ( x2 - 2( m + 3) x + 4) .ex .
Hàm số nghịch biến trên TXĐ khi y’ = ( x2 - 2( m + 3) x + 4) .ex ≤ 0 mọi x

Gọi S là tập hợp các giá trị nguyên của tham số m sao cho hàm số y = x - 1 x - m nghịch biến trên khoảng 4 ; + ∞ . Tính tổng P của các giá trị m của S.
A. P = 10
B. P = 9
C. P = - 9
D. P = - 10
Hình vẽ bên là đồ thị của hàm số y = f(x). Gọi S là tập hợp các số nguyên dương của tham số m để hàm số y = |f(x – 1) + m| có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
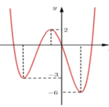
A. 12
B. 15
C. 18
D. 9
Đáp án A.
Phương pháp: Suy ra cách vẽ của đồ thị hàm số y = |f(x – 1) + m| và thử các trường hợp và đếm số cực trị của đồ thị hàm số. Một điểm được gọi là cực trị của hàm số nếu tại đó hàm số liên tục và đổi chiều.
Cách giải: Đồ thị hàm số y = f(x – 1) nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x) sang phải 1 đơn vị nên không làm thay đổi tung độ các điểm cực trị
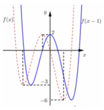
Đồ thị hàm số y = f(x – 1) + m nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x – 1) lên trên m đơn vị nên ta có: yCD = 2 + m; yCT = –3 + m; yCT = –6 + m
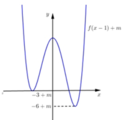
Đồ thị hàm số y = |f(x – 1) + m| nhận được bằng cách từ đồ thị hàm số y = f(x – 1) + m lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
Để đồ thị hàm số có 5 cực trị ![]()
![]()
=>S = {3;4;5} => 3+4+5 = 12
Tìm tất cả các giá trị nguyên của tham số m để hàm số y = x + 1 m 2 x 2 + m − 1 có bốn đường tiệm cận.
A. m<1 và m ≠ 0
B. m < 0
C. m > 1
D. m < 1
Đáp án A
Đồ thị hàm số có bốn tiệm cận ⇔ m 2 x + m − 1 = 0 có hai nghiệm
⇔ m ≠ 0 m − 1 < 0 ⇔ m < 1 ∪ m ≠ 0
3. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+1}{x+3m}\) nghịch biến trên khoảng(6;+\(\infty\) )?
4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (-\(\infty\);-6)?
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Cho hàm số f ( x ) = x 3 - 3 x 2 . Tính tổng tất cả các giá trị nguyên của tham số m để đồ thị của hàm số g ( x ) = f ( | x | ) + m cắt trục hoành tại 4 điểm phân biệt.
A. 3.
B. 10.
C. 4.
D. 6.
Cho hàm số y=\(\sqrt{x+m-1}+\sqrt{m-3x}\).Tìm tất cả các giá trị nguyên của tham số m để hàm số đã cho có tập xác định là R.