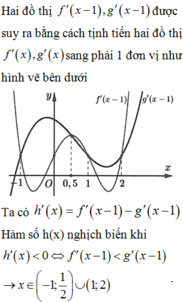
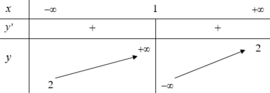
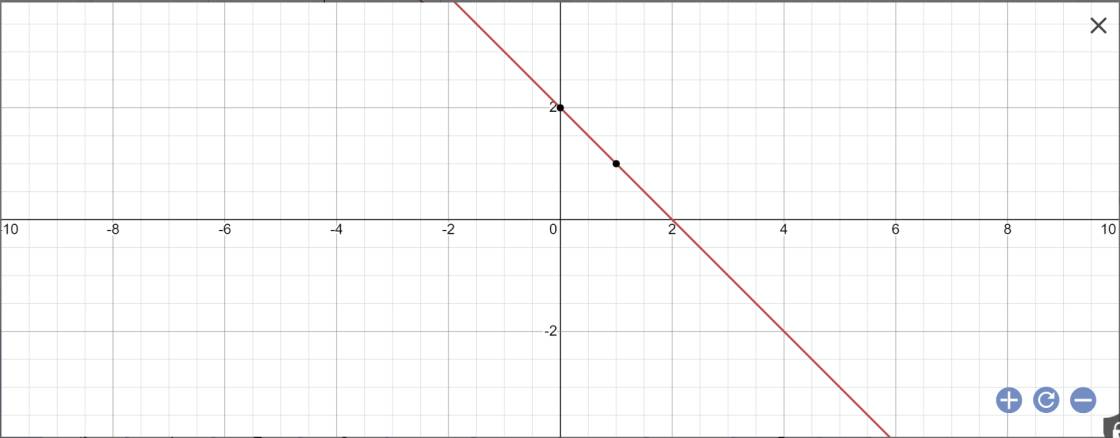
Cho hàm số y = 2 x + 1 x − 1 có đồ thị là (H) và đường thẳng d có hệ số góc m và đi qua điểm A − 2 ; 2 . Giả sử d cắt (H) tại hai điểm phân biệt M, N. Qua M kẻ các đường thẳng lần lượt song song với các trục tọa độ, qua N kẻ các đường thẳng lần lượt song song với các trục tọa độ. Tìm số các giá trị thực của tham số m sao cho bốn đường thẳng đó tạo thành một hình vuông.
A. 0
B. 1
C. 2
D. 3