Giải phương trình bằng cách đặt ẩn phụ:
x + 1 x 2 - 4 . x + 1 x + 3 = 0
giải phương trình căn ( 2x-1) + căn (x-2) = căn (x+1) (bằng cách liên hợp hoặc đặt ẩn phụ)
Đặt: \(\sqrt{2x-1}=a;\sqrt{x-2}=b\Rightarrow\sqrt{x+1}=\sqrt{\left(2x-1\right)-\left(x-2\right)}=\sqrt{a^2-b^2}\)
\(pt\Leftrightarrow a+b=\sqrt{a^2-b^2}\)
\(\Leftrightarrow a^2+2ab+b^2=a^2-b^2\)
\(\Leftrightarrow2b^2+2ab=0\Leftrightarrow2b\left(a+b\right)=0\)
Giải phương trình sau bằng cách đặt ẩn phụ:
\(\dfrac{x}{\sqrt{4x-1}}+\dfrac{\sqrt{4x-1}}{x}=2\)
Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)
Theo đề, ta có phương trình:
a+1/a=2
\(\Leftrightarrow a+\dfrac{1}{a}=2\)
\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)
=>a=1
=>\(x=\sqrt{4x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)
Giải các phương trình sau bằng cách đặt ẩn số phụ x - x - 1 -3 = 0
Đặt m = x - 1 .Điều kiện : m ≥ 0, x ≥ 1
Ta có : x - x - 1 -3 = 0 ⇔ (x -1) - x - 1 -2 =0
⇔ m 2 -m - 2 =0
Phương trình m 2 -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng
a – b + c = 0
Suy ra : m 1 = -1 (loại) , m 2 = -(-2)/1 = 2
Với m =2 ta có: x - 1 =2 ⇒ x -1 =4 ⇔ x =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=5
Giải phương trình bằng cách đặt ẩn phụ:
x x + 1 - 10 . x + 1 x = 3
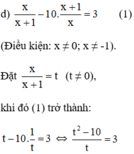
⇔ t2 – 10 = 3t ⇔ t2 – 3t – 10 = 0 (2)
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = (-3)2 - 4.1.(-10) = 49 > 0
⇒ (2) có hai nghiệm:
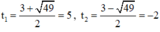
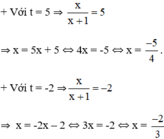
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 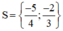
Giải phương trình bằng cách đặt ẩn phụ: x - x = 5 x + 7
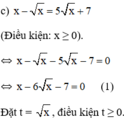
Khi đó (1) trở thành: t2 – 6t – 7 = 0 (2)
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = 7.
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
Giải phương trình bằng cách đặt ẩn phụ: 3 . x 2 + x 2 - 2 x 2 + x - 1 = 0
3.(x2 + x)2 – 2(x2 + x) – 1 = 0 (1)
Đặt t = x2 + x,
Khi đó (1) trở thành : 3t2 – 2t – 1 = 0 (2)
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1; t2 = c/a = -1/3.
+ Với t = 1 ⇒ x2 + x = 1 ⇔ x2 + x – 1 = 0 (*)
Có a = 1; b = 1; c = -1 ⇒ Δ = 12 – 4.1.(-1) = 5 > 0
(*) có hai nghiệm
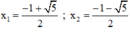
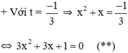
Có a = 3; b = 3; c = 1 ⇒ Δ = 32 – 4.3.1 = -3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 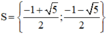
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để đề bài được rõ ràng hơn.
Giải phương trình bằng cách đặt ẩn phụ:
\(\left(x^2+5x+8\right)\left(x^2+6x+8\right)=2x^2\)
\(\Leftrightarrow\left(x^2+8+5x\right)\left(x^2+8+6x\right)=2x^2\)
\(\Leftrightarrow\left(x^2+8\right)^2+11x\left(x^2+8\right)+30x^2-2x^2=0\)
\(\Leftrightarrow\left(x^2+8\right)^2+11x\left(x^2+8\right)+28x^2=0\)
\(\Leftrightarrow\left(x^2+4x+8\right)\left(x^2+7x+8\right)=0\)
\(\Leftrightarrow x^2+7x+8=0\)
\(\text{Δ}=49-32=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-7-\sqrt{17}}{2}\\x_2=\dfrac{-7+\sqrt{17}}{2}\end{matrix}\right.\)
Giải phương trình:
(x+1)\(\sqrt{x^2-2x+3}\)=x2+1
(Giải bằng cách đặt ẩn phụ nha)
ĐK: \(x>-1\)
\(PT\Leftrightarrow a^2-\left(x+1\right)a+2x-2=0\)
\(\Leftrightarrow\left(2-a\right)\left(x-a-1\right)=0\)
.Làm nốt.
~Ko chắc~
À quên: Đặt \(a=\sqrt{x^2-2x+3}\ge\sqrt{2}\)
(x+1)\(\sqrt{x^2-2x+3}\)=\(x^2\)+1
(x+1)\(\sqrt{\left(x-1\right)^2+2}\)-(x+1)(x-1)=0
(x+1)(x-1-x+1+\(\sqrt{2}\))=0
(x+1)\(\sqrt{2}\)=0
<=>x+1=0
<=>x=-1