Cho số nguyên dương n và hệ số của x n - 2 trong khai triển Newton của x - 1 4 n bằng 31.Khi đó n bằng
A. 31
B. 33
C. 32
D. 124
Tìm hệ số của số hạng chứa x 8 trong khai triển nhị thức Newton của 1 x 3 + x 5 n , biết rằng C n + 4 n + 1 - C n + 3 n = 7 ( n + 3 ) . (với n là số nguyên dương và x > 0)
A. 400
B. 480
C. 495
D. 0
Tìm hệ số của x4 trong khai triển Newton của biểu thức \(\left(x^2+\dfrac{2}{x}\right)^n\) ( x khác 0) biết rằng n là số nguyên dương thỏa mản đẳng thức
\(2C^1_n+3C^2_n+4C^3_n+...+\left(n+1\right)C^n_n=111\)
Xét khai triển:
\(\left(1+x\right)^n=C_n^0+C_n^1x+C_n^2x^2+...+C_n^nx^n\)
\(\Leftrightarrow x\left(1+x\right)^n=C_n^0x+C_n^1x^2+C_n^2x^3+...+C_n^nx^{n+1}\)
Đạo hàm 2 vế:
\(\left(1+x\right)^n+nx\left(1+x\right)^{n-1}=C_n^0+2C_n^1x+3C_n^2x^2+...+\left(n+1\right)C_n^nx^n\)
Thay \(x=1\)
\(\Rightarrow2^n+n.2^{n-1}=1+2C_n^1+3C_n^2+...+\left(n+1\right)C_n^n\)
\(\Rightarrow2^{n-1}\left(2+n\right)-1=111\)
\(\Rightarrow2^{n-1}\left(2+n\right)=112=2^4.7\)
\(\Rightarrow n=5\)
\(\left(x^2+\dfrac{2}{x}\right)^5=\sum\limits^5_{k=0}C_5^kx^{2k}.2^{5-k}.x^{k-5}=\sum\limits^5_{k=0}C_5^k.2^{5-k}.x^{3k-5}\)
\(3k-5=4\Rightarrow k=3\Rightarrow\) hệ số: \(C_5^3.2^2\)
Cho khai triển nhị thức Newton của 2 − 3 x 2 n , biết rằng n là số nguyên dương thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + C 2 n + 1 5 + ... + C 2 n + 1 2 n + 1 = 1024. .
Hệ số của x 7 bằng
A. -2099520
B. -414720
C. 2099520
D. 414720
Đáp án là A
• Xét khai triển:
x + 1 2 n + 1 = C 2 n + 1 0 x 2 n + 1 + C 2 n + 1 1 x 2 n + ... + C 2 n + 1 2 n + 1 .
Cho x = 1 , ta được: 2 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 . (1)
Cho x = − 1 , ta được: 0 = − C 2 n + 1 0 + C 2 n + 1 1 − ... + C 2 n + 1 2 n + 1 . (2)
Cộng (1) và (2) vế theo vế, ta được:
2 2 n + 1 = 2 C 2 n + 1 1 + C 2 n + 1 3 + ... + C 2 n + 1 2 n + 1 ⇔ 2 2 n + 1 = 2.1024 ⇔ n = 5
• Xét: 2 − 3 x 10 = ∑ 0 10 C 10 k 2 10 − k . − 3 x k = ∑ 0 10 − 3 k .2 10 − k . C 10 k . x k
Hệ số của x 7 là: − 3 7 .2 3 . C 10 7 = − 2099520.
Cho khai triển nhị thức Newton của 2 - 3 x 2 n , biết rằng n là số nguyên dương thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + C 2 n + 1 5 + . . . + C 2 n + 1 2 n + 1 = 1024 .
Hệ số của x 7 bằng
A. -2099520
B. -414720
C. 2099520
D. 414720
Cho n là số nguyên dương thỏa mãn A n + 3 3 - 6 C n + 1 3 = 294
Tìm số hạng mà tích số mũ của x và y bằng 18 trong khai triển nhị thức Newton: 6 n . x 4 3 y + y 2 x 2 n (với x ≠ 0 ; y ≠ 0 ).
A. 160 x 9 y 2
B. 160 x 2 y 9
C. 160 x 3 y 6
D. 160 x 6 y 3
Điều kiện: 2 ≤ n ∈ N
Ta có
A n + 3 3 - 6 C n + 1 3 = 294 ⇔ n + 3 ! n ! - 6 n + 1 ! 3 ! n - 2 ! = 294 ⇔ n + 3 n + 2 n + 1 - n + 1 n n - 1 = 294 ⇔ n 2 + 2 n - 48 = 0 ⇔ n = 6 n = - 8
So với điều kiện chọn n = 6
Với n = 6 ta có 2 x 4 y + y 2 x 2 6 = ∑ k = 0 6 C 0 k 2 x 4 y 6 - k y 2 x 2 k = ∑ k = 0 6 C 0 k 2 6 - k x 24 - 6 k y - 6 + 3 k
Giả thiết bài toán cho ta 24 - 6 k - 6 + 3 k = 18 ⇔ k - 3 2 = 0 ⇔ k = 3
Khi k = 3 ta thu được số hạng thỏa mãn yêu cầu bài toán là: C 6 3 2 2 x 6 y 3 = 160 x 6 y 3
Đáp án D
Cho n là số nguyên dương sao cho tổng các hệ số trong khai triển của x + 1 n bằng 1024. Hệ số của x 8 trong khai triển đó bằng
A. 2 8
B. 90
C. 45
D. 80
Cho số n nguyên dương và thỏa mãn C n 0 + 2 C n 1 + 4 C n 2 + . . . . + 2 n C n n = 243 Tìm hệ số của x 2 trong khai triển ( 1 + x ) n
A. 4
B. 5
C. 15
D. 10
Cho khai triển ( 1 + x ) n với n là số nguyên dương. Tìm hệ số của số hạng chứa x 3 trong khai triển biết C 2 n + 1 1 + C 2 n + 1 2 + C 2 n + 1 3 + . . . . . + C 2 n + 1 n = 2 20 - 1 .
A. 480
B. 720
C. 240
D. 120
Chọn D
Ta có: ![]()

Ta có: 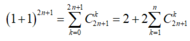
![]()
Hệ số của số hạng chứa x 3 là: C 10 3 = 120.
Tìm sô hạng không chứa x trong khai triển x 2 + 1 x n (x ¹ 0 và n là số nguyên dương), biết rằng tổng các hệ số của số hạng thứ nhất, thứ hai và thứ ba trong khai triển bằng 46
A. 84
B. 62
C. 86
D. 96