Cho một cấp số cộng có u 1 = - 3 ; u 6 = 27 . Tìm công sai d?
A. d = 5
B. d = 7
C. d = 6
D. d = 8
1. Cho 3 số lập thành cấp số cộng. Biết tổng 3 số bằng 6 và tổng bình phương 3 số bằng 30. Tìm các số.
2. Tìm m để phương trình sau có 4 nghiệm lập thành cấp số cộng:
\(x^4-10x^2+9m=0\)
3. Cho cấp số cộng giảm thỏa mãn:
\(\left\{{}\begin{matrix}u_1+u_2+u_3=3\\u_3^2-u_2^2=3\end{matrix}\right.\)
Tính: \(S=\dfrac{1}{u_1u_2}+\dfrac{1}{u_2u_3}+...+\dfrac{1}{u_{19}u_{20}}\)
4. Cho cấp số cộng tăng:
\(\left\{{}\begin{matrix}u_1+u_3+u_5=-3\\u_2+u_4+u_6=3\end{matrix}\right.\)
Tính: \(S=u_1+u_4+u_7+...+u_{88}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn mọi người nhiều!!!
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
1) tìm số hạng đầu và công sai của một cấp số cộng biết \(\left\{{}\begin{matrix}u_3=-3\\u_9=29\end{matrix}\right.\)
2) cho cấp số cộng \(\left(u_n\right)\) có \(u_1=-5\) và d = 3. Tính \(S_{20}\)
1: u3=-3 và u9=29
=>u1+2d=-3 và u1+8d=29
=>-6d=-32 và u1+2d=-3
=>d=16/3 và u1=-3-2d=-3-32/3=-41/3
2: \(S_{20}=\dfrac{20\cdot\left[2\cdot u1+19\cdot d\right]}{2}=10\cdot\left(-5\cdot2+19\cdot3\right)\)
=10(57-10)
=10*47=470
Cho cấp số cộng \(u_1,u_2,u_3,...,u_n\) có công sai d, các số hạng của cấp số cộng đã cho đều khác 0. Với giá trị nào của d thì dãy số \(\dfrac{1}{u_1};\dfrac{1}{u_2};\dfrac{1}{u_3};...;\dfrac{1}{u_n}\) là một cấp số cộng?
Cho cấp số cộng \(u_1,u_2,u_3,...,u_n,...\) có công sai bằng 3. Biết dãy \(u_1,u_3,u_5,...,u_{2n+1}\) là cấp số cộng. Tính công sai của cấp số cộng đó?
Công sai của cấp số cộng đó là:
\(u_3-u_1=u_1+2d-u_1=2d=2\cdot3=6\)
Cho u n là một cấp số cộng có sáu số hạng với u 1 = ( - 1 ) / 3 , d = 3 . Viết dạng khai triển của nó.
Dạng khai triển của cấp số cộng đó là:
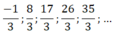
cho (Un) là cấp số cộng U3 +U13=80 .tổng 15 số hạng đầu tiên của cấp số cộng đố bằng bao nhiêu
Ba số nguyên dương lập thành một cấp số cộng khi một số bất kì bằng trung bình cộng của hai số còn lại. Hãy viết 1 chương trình kiểm tra ba số a,b,c có lập thành cấp số cộng không? GIÚP CỢI Ạ <3
#include <bits/stdc++.h>
using namespace std;
long long a,b,c;
bool kt;
int main()
{
cin>>a>>b>>c;
kt=false;
if (a==(b+c)/2) kt=true;
if (b==(a+c)/2) kt=true;
if (c==(b+a)/2) kt=true;
if (kt==false) cout<<"Khong lap duoc";
else cout<<"Lap duoc";
return 0;
}
Cho một cấp số cộng có u 1 = − 3 ; u 6 = 27 . Tìm d ?
A. d=5
B. d=6
C. d=7
D. d=8
Ta có:
u 6 = 27 ⇔ u 1 + 5 d = 27 ⇔ − 3 + 5 d = 27 ⇔ 5 d = 30 ⇔ d = 6
Chọn đáp án B
Cho một cấp số cộng có u 1 = − 3 ; u 6 = 27 . Tìm d ?
A. d= 5
B. d= 7
C. d =6
D. d= 8
Chọn C
u 6 = 27 ⇔ u 1 + 5 d = 27 ⇔ − 3 + 5 d = 27 ⇔ 5 d = 30 ⇔ d = 6