Tính nhanh
80 x 33 + 97 x 33 + 34 x 97 + 33 x17
Nhanh mình tich cho
tính nhanh : 33 x 97 + 99
33 x 97 + 99
= 33 x 97 + 33 x 3
= 33 x (97 + 3)
= 33 x 100
= 3300
33x97+99
=33x97+33x3
=33x(97+3)
=33x100
=3300
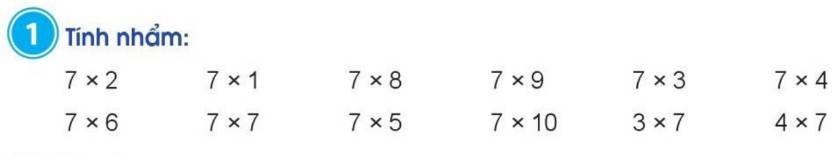
Tính nhẩm:
7 x 2
7 x 6
7 x 1
7 x 7
7 x 8
7 x 5
7 x 9
7 x 10
7 x 3
3 x 7
7 x 4
4 x 7
Không tính hãy so sánh
M=21 x 120 và N=33 x 80
P=93 x 591 và Q=97 x 551
H =27.28281và F=28 x 272271
a: \(M=21\cdot120=120\cdot21\)
\(N=33\cdot80=120\left(11\cdot2\right)\)
mà 21<11x2
nên M<N
56 x 33 = ? 46 x 32 = ?
88 x 88 = ? 67 x 43 = ?
97 x 45 = ? 30 x 15 = ?
56 x 33= 1848
88 x 88= 7744
97 x 45= 4365
46 x 33= 1518
67 x 43= 2881
30 x 15= 450
Không tính hãy so sánh
M=21 x 120 và N=33 x 80
P=93 x 591 và Q=97 x 551
H =27.28281và F=28 x 272271
Tìm X
(X+1)+(x+2)+...+(x+20)=310
a: \(M=21\cdot120=21\cdot120\)
\(N=33\cdot80=120\left(11\cdot2\right)\)
mà \(21< 11\cdot2\)
nên M<N
tính x=\(\sqrt{97-56\sqrt{3}}+\sqrt{52+16\sqrt{3}}\)
y=\(\sqrt{33+20\sqrt{2}}+\sqrt{24-16\sqrt{2}}\)
Ta có: \(x=\sqrt{97-56\sqrt{3}}+\sqrt{52+16\sqrt{3}}\)
\(=\sqrt{49-2\cdot7\cdot4\sqrt{3}+48}+\sqrt{48+2\cdot4\sqrt{3}\cdot2+4}\)
\(=\sqrt{\left(7-4\sqrt{3}\right)^2}+\sqrt{\left(4\sqrt{3}+2\right)^2}\)
\(=\left|7-4\sqrt{3}\right|+\left|4\sqrt{3}+2\right|\)
\(=7-4\sqrt{3}+4\sqrt{3}+2\)
\(=9\)
Làm luôn phần y :D
y = \(\sqrt{33+20\sqrt{2}}+\sqrt{24-16\sqrt{2}}\)
y = \(\sqrt{33+2.10\sqrt{2}}+\sqrt{24-2.8\sqrt{2}}\)
y = \(\sqrt{33+2.5.2\sqrt{2}}+\sqrt{24-2.4.2\sqrt{2}}\)
y = \(\sqrt{25+2.5.\sqrt{8}+8}+\sqrt{16-2.4.\sqrt{8}+8}\)
y = \(\sqrt{\left(5+\sqrt{8}\right)^2}+\sqrt{\left(4-\sqrt{8}\right)^2}\)
y = |5 + \(\sqrt{8}\)| + |4 - \(\sqrt{8}\)|
y = 5 + \(\sqrt{8}\) + 4 - \(\sqrt{8}\) (Vì 4 > \(\sqrt{8}\) nên 4 - \(\sqrt{8}\) > 0)
y = 9
Vậy y = 9
Chúc bn học tốt!
Tính nhanh:29+31+33+...+97.Ai nhanh giúp mình với
Giải phương trình : (3/1*3+3/3*5+....+3/97*99)(2x+1)=x+1/33
tính bằng cách thuận tiện nhất :
a) (3/13 x 17/29 ) x 29/34 = ??
b) 4/21 x 19/33 + 25/42 x 19/33 =??
a,=3/13.17/29.29/34
=3/13.1/2
=3/26
b,=(4/21+25/42).19/33
=11/14.19/33
=19/42
`a, = 3/13 xx (17/29 xx 29/34)`
`= 3/13 xx 1/2`
`= 3/26`.
`b, = 19/33(4/21 + 25/42)`
`= 19/33 xx ( 33/42 )`
`= 19/42`
`a)(3/13xx17/29)xx29/34=3/13xx17/29xx29/34=[3xx17xx29]/[13xx19xx17xx2]=3/26`
`b)4/21xx19/33+25/42xx19/33=19/33xx(4/21+25/42)=19/33xx(8/42+25/42)=19/33xx33/42=19/42`