Tìm các số nguyên x,y thỏa mãn : x + y + xy = 12
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm các số nguyên x,y thỏa mãn : xy +12=x+y
Lời giải:
$xy+12=x+y$
$\Rightarrow xy-x-y=-12$
$\Rightarrow x(y-1)-y=-12$
$\Rightarrow x(y-1)-(y-1)=-11$
$\Rightarrow (y-1)(x-1)=-11$
Do $x,y$ nguyên nên $x-1,y-1$ cũng nguyên. Ta có bảng: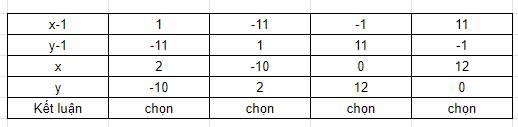
Tìm các số nguyên dương x;y;z thỏa mãn: xy(x+y)=6;yz(y+z)=12;zx(z+x)=30
Bài 4. Tìm các số nguyên x và y thỏa mãn (x+1).( y-2) =5 Bài 5. Tìm các số nguyên x và y thỏa mãn xy -2x + 3y
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Tìm các cặp số nguyên(x;y) thỏa mãn x+y=xy; 2(x+y)=xy
a)Tìm các số nguyên dương x, y thỏa mãn x+3 chia hết cho y, y+3 chia hết cho x
b)Tìm các số nguyên dương x, y thỏa mãn xy+x+y+2 chia hết cho cả x và y.
Tìm các số nguyên x,y thỏa mãn:
xy-x+y=1
\(xy\) - \(x\) + \(y\) = 1
(\(xy\) + \(y\)) - \(x\) - 1 = 0
\(y\)(\(x\) + 1) - ( \(x\) + 1) = 0
(\(x\) + 1)( \(y\) - 1) = 0
\(\left[{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)