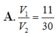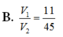Cho hình lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Cho hình lăng trụ ABC.A'B'C' Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Đáp án A
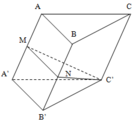
V A A ' B ' C ' = V C ' A B C = V A B B ' C ' = 1 3 V A B C A ' B ' C ' V M N A ' B ' C ' = 1 2 V C ' A B B ' A ' = 1 2 . ( V A A ' B ' C ' + V A B B ' C ' ) = 1 2 . 2 3 V A B C A ' B ' C ' = 1 3 V A B C A ' B ' C ' ⇒ V M N C ' A B C V M N A ' B ' C ' = 2
Cho hình lăng trụ ABC.A'B'C' có A'.ABC là tứ diện đều cạnh a. Gọi M,N lần lượt là trung điểm của AA' và BB'. Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).
A. 2 5
B. 3 2 4
C. 2 2 5
D. 4 2 5
Cho hình lăng trụ ABC.A'B'C' có A'.ABC là tứ diện đều cạnh a. Gọi M, N lần lượt là trung điểm của AA' và BB' Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).
A . 2 5
B . 2 2 5
C . 3 2 4
D . 2 3
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB', CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Đáp án B.
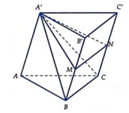
Vì M,N lần lượt là trung điểm của BB' và CC' nên ta có:
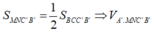
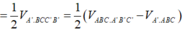
Lại có:
![]()

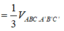
Vậy tỉ số
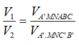
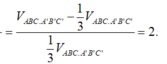
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB',CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B , V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Đáp án B
Vì M,N lần lượt là trung điểm của BB' và CC' nên ta có:
S M N C ' B ' = 1 2 S B C C ' B ' ⇒ V A ' . M N C ' B ' = 1 2 V A ' . B C C ' B ' = 1 2 V A B C . A ' B ' C ' - V A ' . A B C
Lại có:
V A ' . A B C = 1 3 V A B C . A ' B ' C ' ⇒ V A ' . M N C ' B ' = 1 2 V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' = 1 3 V A B C . A ' B ' C '
Vậy tỉ số V 1 V 2 = V A ' M N A B C V A ' . M N C ' B ' = V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' 1 3 V A B C . A ' B ' C ' = 2
Cho hình lăng trụ A B C . A ' B ' C ' . Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA', BB', CC' sao cho A M = 2 M A ' , N B ' = 2 N B , P C = P C ' . Gọi V 1 , V 2 lần lượt là thể tích của hai khối đa diện ABCMNP và A ' B ' C ' M N P . Tính tỷ số V 1 V 2
A. V 1 V 2 = 2
B. V 1 V 2 = 1 2
C. V 1 V 2 = 1
D. V 1 V 2 = 2 3
Cho lăng trụ A B C . A ' B ' C ' có thể tích V, gọi M, N lần lượt là trung điểm các cạnh BB', CC'. Tính thể tích khối chóp A . B C M N theo V.
A. V 2
B. V 3
C. 2 V 3
D. V 6
Cho lăng trụ ABC.A’B’C’ có thể tích V, gọi M, N, P lần lượt thuộc cạnh AA’; BB’; CC’ sao cho 2 M A = M A ' , N B = N B ' ; 3 P C = P C ' . Mặt phẳng chia khối lăng trụ A B C . A ' B ' C ' thành hai phần. Tính tỉ số thể tích hai phần này (số bé chia số lớn).
A. 17 19
B. 17 36
C. 13 23
D. 13 36
Chọn đáp án C
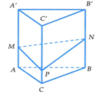
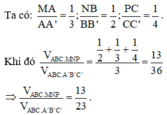
Chú ý: Trong bài toán trên ta sử dụng công thức tính nhanh sau:



Cho lăng trụ đứng tam giác ABC.A'B'C'. Gọi M, N, P, Q là các điểm thuộc các cạnh AA', BB', CC' thỏa mãn A M A A ' = 1 2 , B N B B ' = 1 3 , C P C C ' = 1 4 , C ' Q C ' B ' = 1 5 . Gọi V1, V2 lần lượt là thể tích khối tứ diện MNPQ và khối lăng trụ ABC.A'B'C'. Tính tỷ số V 1 V 2 .