Gọi z 1 và z 2 = 4 + 2 i là hai nghiệm của phưong trình a z 2 + b z + c = 0 ( a , b , c , ∈ ℝ , a ≠ 0 ) Tính T = z 1 + 3 z 2
A. T = 6
B. T = 4 5
C. T = 2 5
D. T = 8 5
PB
Những câu hỏi liên quan
Gọi
z
1
,
z
2
,
z
3
,
z
4
là nghiệm của phương trình
(
z
-
1
2
z
-
i...
Đọc tiếp
Gọi z 1 , z 2 , z 3 , z 4 là nghiệm của phương trình ( z - 1 2 z - i ) 4 =1. Giá trị của ( z 1 . z 2 . z 3 . z 4 ) 2 bằng
A. 2i
B. i
C. 0
D. -1
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
Nếu z1-i và z1 là 2 nghiệm của phương trình thì
a
-
b
-
c
bằng A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Tìm giá trị nhỏ nhất nhất của bấc phưong trình sau : 2(3-z)-3(2+z)≤z
\(\Leftrightarrow6-2z-6-3z\le z\)
\(\Leftrightarrow6z\ge0\)
\(\Rightarrow z\ge0\)
\(\Rightarrow z_{min}=0\)
Đúng 1
Bình luận (0)
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
. Nếu
z
1
−
i
và
z
1
là hai nghiệm của phương trình thì
a
−
b
−
c
bằng (a, b, c là số thực). A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Số nghiệm phức của phương trình
z
+
2
|
z
|
+
3
-
i
(
4
+
i
)
|
z
|...
Đọc tiếp
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
2
và
z
1
+
i
làm các nghiệm của phương trình. Khi đó
a
-
b
+
c
là
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
A. 0,5
B. 1,5
C. 1
D. 2
Chọn B.
Phương trình đã cho tương đương với:
( z – 2i) ( z – 1 – i) = 0
Suy ra: z = 2i hoặc z = 1 + i
Do | z1| > | z2|. nên ta có z1 = 2i và z2 = 1 + i
Ta có
Đúng 0
Bình luận (0)
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
3
z
2
-
z
+
2
0
. Tính
|
z
1
|
2
+
|
z
2
|
2
A. -11/9 B. 8/3 C. 2/3 D. 4/3
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính | z 1 | 2 + | z 2 | 2
A. -11/9
B. 8/3
C. 2/3
D. 4/3
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
- z + 2. Tính
z
1
2
+
z
2
2
A.
-
11
9...
Đọc tiếp
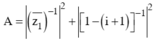
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 - z + 2. Tính z 1 2 + z 2 2
A. - 11 9
B. 8 3
C. 2 3
D. 4 3
