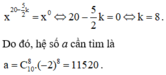Biết tổng các hệ số trong khai triển 3 x - 1 n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n là 2 11 . Tìm a 6 .
A. a 6 = - 336798
B. a 6 = 336798
C. a 6 = - 112266
D. a 6 = 112266
Biết tổng các hệ số của ba số hạng đầu trong khai triển \(\left(x^3+\dfrac{1}{x^2}\right)^n\) bằng 11. Tìm hệ số của \(x^7\) trong khai triển đó.
\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)
Biết tổng các hệ số của khai triển \(\left(3-x^2\right)^n\)bằng 1024. Hệ số của số hạng chứa \(x^{12}\) trong khai triển đó bằng bao nhiêu?
\(\left(3-1\right)^n=1024\Leftrightarrow2^n=2^{10}\Rightarrow n=10\)
\(\left(3-x^2\right)^{10}\) có SHTQ: \(C_{10}^k.3^k.\left(-1\right)^{10-k}.x^{20-2k}\)
Số hạng chứa \(x^{12}\Rightarrow20-2k=12\Rightarrow k=4\)
Hệ số: \(C_{10}^4.3^4=...\)
Trong khai triển ( 1 + x ) n biết tổng các hệ số C n 1 + C n 2 + C n 3 + . . . . + C n n - 1 = 126 . Hệ số của x 3 bằng
A. 15
B. 21
C. 35
D. 20
Chọn C
Ghi nhớ: Với khai triển nhị thức:
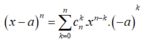
(Với a
≠
0 là hằng số) thì hệ số của ![]()
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
Tìm hệ số của \(x^6\) trong khai triển \(\left(\frac{1}{x}+x^3\right)^n\) biết tổng các hệ số trong khai triển là 1024.
\(\left(\frac{1}{x}+x^3\right)^n=\sum\limits^n_{k=0}C^{n-k}_n\left(\frac{1}{x}\right)^{n-k}.\left(x^3\right)^k\)
Tổng các hệ số: \(C^0_n+C^1_n+...+C^n_n=\left(1+1\right)^n=2^n=1024\)
=> n = 10
Cho khai triển 1 + x 2 n biết tổng của tất cả các hệ số trong khai triển đã cho bằng 1024. Tìm n.
A. n = 9
B. n = 10
C. n = 11
D. n = 12
Biết tổng các hệ số của ba số hạng đầu trong khai triển ( x 2 - 2 x ) n bằng 49. Khi đó hệ số của số hạng chứa x 3 trong khai triển đó là:
A.60 x 3 .
B.60.
C.-160.
D.-160 x 3
Cho n là số nguyên dương sao cho tổng các hệ số trong khai triển của x + 1 n bằng 1024. Hệ số của x 8 trong khai triển đó bằng
A. 2 8
B. 90
C. 45
D. 80
Tìm sô hạng không chứa x trong khai triển x 2 + 1 x n (x ¹ 0 và n là số nguyên dương), biết rằng tổng các hệ số của số hạng thứ nhất, thứ hai và thứ ba trong khai triển bằng 46
A. 84
B. 62
C. 86
D. 96
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + … + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n (n là số nguyên dương).
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a = 11250
C. a = 12150
D. a = 10125
Đáp án A
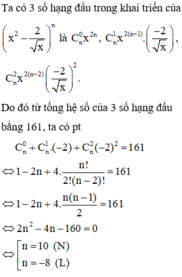
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
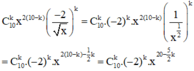
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho