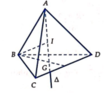
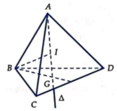
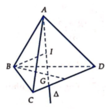
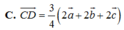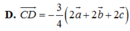Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt x → = A B → , y → = A C → , z → = A D → . Khẳng định nào sau đây là khẳng định đúng?
A. A G → = 1 3 ( x → + y → + z → )
B. A G → = - 1 3 ( x → + y → + z → )
C. A G → = 2 3 ( x → + y → + z → )
D. A G → = - 2 3 ( x → + y → + z → )