Đáp án A.
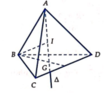
Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất
![]()
![]()
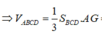
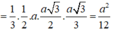
Đáp án A.

Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất
![]()
![]()
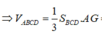
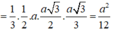
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC
A. V=3
B. V=4
C. V=5
D. V=6
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
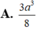
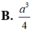
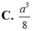
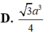
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
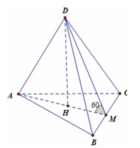
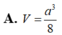
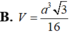
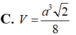
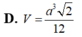
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
A. a r c sin 33 40
B. a r c sin 11 40
C. a r c cos 33 40
D. a r c cos 11 40
Cho tứ diện đều ABCD cạnh bằng a. Diện tích xung quanh Sxq của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện ABCD là
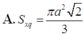
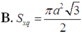
![]()
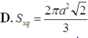
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O,AB=a,AD=a căn 3 , tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm SA, G là trọng tâm tam giác SCD, Thể tích khối tứ diện DOGM bằng
Cho tứ diện ABCD đều cạnh 3a. Tính diện tích xung quanh của hình nón có đỉnh là A, đường tròn đáy là đường tròn ngoại tiếp tam giác BCD.
A. 3 3 πa 2
B. 3 2 πa 2 2
C. 3 3 πa 2 2
D. 9 πa 2 4
Tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng (BCD), AB = 2a. M là trung điểm của AD, gọi φ là góc giữa đường thẳng CM với mp(BCD), khi đó
A. tan φ = 3 2
B. tan φ = 2 3 3
C. tan φ = 3 2 2
D. tan φ = 6 3