Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là:
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
PB
Những câu hỏi liên quan
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy
I
∈
A
C
,
J
∈
D
N
sao cho IJ // BM. Độ dài IJ theo a là A.
a
3
3
B.
a
2
3
C.
a...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
JE
28 tháng 1 2021 lúc 22:31
Cho tứ diện đều ABCD có cạnh a. Gọi M, N lần lượt là trung điểm của AB, CD. Tính độ dài đoạn MN theo a
Lời giải:Tam giác $BCD, ACD$ đều và $N$ là trung điểm $CD$ nên dễ dàng tính được $AN=BN=\frac{\sqrt{3}a}{2}$
$\Rightarrow \triangle ABN$ là tam giác cân tại $N$
Do đó đường trung tuyến $NM$ đồng thời là đường cao.
Áp dụng định lý Pitago:
$MN=\sqrt{BN^2-BM^2}=\sqrt{BN^2-(\frac{AB}{2})^2}$
\(=\sqrt{(\frac{\sqrt{3}a}{2})^2-(\frac{a}{2})^2}=\frac{\sqrt{2}}{2}a\)
Đúng 0
Bình luận (0)
BT
29 tháng 10 2016 lúc 21:42
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .
BT
29 tháng 10 2016 lúc 18:15
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .
BT
8 tháng 11 2016 lúc 18:14
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó
BT
3 tháng 11 2016 lúc 18:29
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .
BT
30 tháng 10 2016 lúc 9:28
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .
BT
5 tháng 11 2016 lúc 23:20
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .
BT
28 tháng 10 2016 lúc 19:58
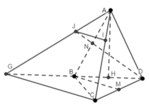
cho tứ diện đều ABCD cạnh a . Gọi I , J lần lượt là trung điểm của AB và CD .
gọi G là trọng tâm tam giác ACD, M là trung điểm BC . tính các tỉ số mà mặt phẳng (IGM) chia các cạnh CD , AD . xác định thiết diện của tứ giác ABCD với mặt phẳng (IGM) . thiết diện là hình gì ? tính diện tích thiết diện đó .