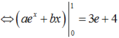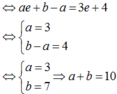tỉ số của a và b là 4/5 nếu a = 24 thì b có giá trị là
LV
Những câu hỏi liên quan
Tỉ số của a và b là 3/5 nếu a = 24 thì b có giá trị là
A. b = 25 B. b = 35 C. b = 30 D. b = 40
a, Biết rằng y1 tỉ lệ thuận với x1 theo hệ số tỉ lệ a; y2 tỉ lệ thuận với x2 cũng theo hệ số tỉ lệ a.Hỏi y1+y2 có tỉ lệ thuannj với x1+x2 không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
b,Cho x,y là 2 đại lượng tỉ lệ thuận . Khi giá trị x1 , x2 của x có tổng bằng 5 thì 2 giá trị tương ứng của y1 , y2 có tổng là 35.Tính giá trị của y khi x=-4.
Nếu các số hữu tỉ a;b thỏa mãn
∫
0
1
a
e
x
+
b
d
x
3
e
+
4
thì giá trị của biểu thức
a
+
b
là A. 10 B. 8 C. 9 D. 7
Đọc tiếp
Nếu các số hữu tỉ a;b thỏa mãn ∫ 0 1 a e x + b d x = 3 e + 4 thì giá trị của biểu thức a + b là
A. 10
B. 8
C. 9
D. 7
a*b*c là biểu thức có chứa 3 chữ số
Nếu a =4,b=3 và c=5 thì giá trị của biểu thức a*b*c là:a*b*c=4*3*5=12*5=60
Chó con số a/b có giá trị bằng 5/3.Nếu thêm 8 đơn vị vào mỗi số(b) và giữ nguyên tử số (a) thì được phân số mới có giá trị là 3/4.Tìm a/b
Viết số thích hợp vào chỗ chấm (theo mẫu)a) Nếu a 10 thì 65 + a 65 + … .Giá trị của biểu thức 65 + a với a 10 là ………….b) Nếu b 7 thìGiá trị của biểu thức với b 7 là …………c) Nếu m 6 thìGiá trị của biểu thức với m 6 là ……….d) Nếu n 5 thì Giá trị của biểu thức 185 : n với n 5 là ……..
Đọc tiếp
Viết số thích hợp vào chỗ chấm (theo mẫu)
a) Nếu a = 10 thì 65 + a = 65 + … =.
Giá trị của biểu thức 65 + a với a = 10 là ………….
b) Nếu b = 7 thì
Giá trị của biểu thức với b = 7 là …………
c) Nếu m = 6 thì
Giá trị của biểu thức với m = 6 là ……….
d) Nếu n = 5 thì
Giá trị của biểu thức 185 : n với n = 5 là ……..
a) Nếu a = 10 thì 65 + a = 65 + 10 = 75.
Giá trị của biểu thức 65 + a với a = 10 là 75.
b) Nếu b = 7 thì 185 – b = 185 – 7 = 178.
Giá trị của biểu thức 185 – b với b = 7 là 178.
c) Nếu m = 6 thì 423 + m = 423 + 6 = 429.
Giá trị của biểu thức 423 + m với m = 6 là 429.
d) Nếu n = 5 thì 185 : 5 = 37.
Giá trị của biểu thức 185 : n với n = 5 là 37.
Đúng 2
Bình luận (0)
a)Nếu x;y;z tỉ lệ thuận với a,b,c thì ta có?
Nếu x;y;z tỉ lệ nghịch với a,b,c thì ta có?
b) Cách tính giá trị của hàm số tại 1 giá trị cho trước của biển.
c)Cách tìm giá trị của biến số khi biết giá trị của hàm số.
d) Nếu điểm nằm trên đồ thị hàm số thì tọa độ của nó thỏa mãn công thức của hàm số.
e) Cách kiểm tra một điểm có tọa độ cho trước có thuộc đồ thị hàm số không.
Đọc tiếp
a)Nếu x;y;z tỉ lệ thuận với a,b,c thì ta có? Nếu x;y;z tỉ lệ nghịch với a,b,c thì ta có? b) Cách tính giá trị của hàm số tại 1 giá trị cho trước của biển. c)Cách tìm giá trị của biến số khi biết giá trị của hàm số. d) Nếu điểm nằm trên đồ thị hàm số thì tọa độ của nó thỏa mãn công thức của hàm số. e) Cách kiểm tra một điểm có tọa độ cho trước có thuộc đồ thị hàm số không.
a: x,y,z tỉ lệ thuận với a,b,c
thì x/a=y/b=z/c
x,y,z tỉ lệ nghịch với a,b,c
nên ax=yb=cz
b: Chỉ cần thay giá trị của biến vào hàm số
c: Đặt hàm số có giá trị bằng giá trị cho trước xong rồi tìm giá trị của biến
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:1. Nếu hàm số
y
f
x
liên tục, có đạo hàm tới cấp hai trên
a
;
b
,
x
0
∈
a
;
b
và
f
x...
Đọc tiếp
Cho các mệnh đề sau:
1. Nếu hàm số y = f x liên tục, có đạo hàm tới cấp hai trên a ; b , x 0 ∈ a ; b và f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x0 là một điểm cực trị của hàm số.
2. Nếu hàm số y = f x xác định trên a ; b thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
3. Nếu hàm số y = f x liên tục trên a ; b thì hàm số có đạo hàm tại mọi x thuộc [a;b].
4. Nếu hàm số y = f x có đạo hàm trên a ; b thì hàm số có nguyên hàm trên a ; b
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Đáp án A.

Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]
Đúng 0
Bình luận (0)
n là số nguyên dương và k là tích của tất cả các số nguyên từ 1 đến n. Nếu k là bội số của 1440 thì giá trị nhỏ nhất có thể có của n là A. 8 B. 12 C. 16 D. 18 E. 24
Lời giải:
$1440=2^5.3^2.5$
Để $k=n!\vdots 1440$ thì $n!\vdots 2^5$; $n!\vdots 3^2; n!\vdots 5$
Để $n!\vdots 3^2; 5$ thì $n\geq 6(1)$
Để $n!\vdots 2^5$. Để ý $2=2^1, 4=2^2, 6=2.3, 8=2^3$. Để $n!\vdots 2^5$ thì $n\geq 8(2)$
Từ $(1); (2)$ suy ra $n\geq 8$. Giá tri nhỏ nhất của $n$ có thể là $8$
Đúng 1
Bình luận (0)