Gọi x1, x2, x3 lần lượt là hoành độ giao điểm của đồ thị hai hàm số f x = x 3 - 3 x 2 + 2 x + 2 và g x = 3 x - 1 . Tính giá trị của biểu thức S = f x 1 + g x 2 + f x 3
A. S = 14
B. S = 1
C. S = 6
D. S = 3
PB
Những câu hỏi liên quan
Giả sử đồ thị (C) của hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai điểm cực trị là
M
(
-
1
;
7
)
và
N
(
5
;
-
7
)
. Gọi
x
1
;
...
Đọc tiếp
Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M ( - 1 ; 7 ) và N ( 5 ; - 7 ) . Gọi x 1 ; x 2 ; x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2
Giả sử đồ thị (C) của hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai điểm cực trị là
M
-
1
;
7
v
à
N
5
;...
Đọc tiếp
Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M - 1 ; 7 v à N 5 ; - 7 . Gọi x 1 , x 2 , x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2
Chọn A.
Phương pháp : Lập hệ tìm a, b, c, d sau đó sử dụng định lý Viet để tính.
Đúng 0
Bình luận (0)
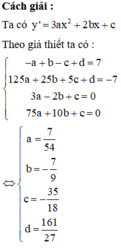
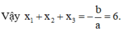
2) Cho hàm số 2 y=x2 có đồ thị là parabol (P), hàm số y=(m- 2)x- m+3 có đồ thị là đường thẳng (d).a) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt.b) Gọi A và B là hai giao điểm của (d) và (P), có hoành độ lần lượt là x1 ; x2 . Tìm các giá trị của m để x1,x2 là độ dài hai cạnh của một tam giác vuông cân.
a, - Xét phương trình hoành độ giao điểm :\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\left(I\right)\)
Có \(\Delta=b^2-4ac=\left(m-2\right)^2-4\left(m-3\right)\)
\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)
- Để P cắt d tại 2 điểm phân biệt <=> PT ( I ) có 2 nghiệm phân biệt .
<=> \(\Delta>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
\(\Leftrightarrow m\ne4\)
Vậy ...
b, Hình như đề thiếu giá trị của cạnh huỳnh hay sao á :vvvv
Đúng 2
Bình luận (0)
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\)
\(\Delta=\left(m-2\right)^2-4\cdot\left(m-3\right)=m^2-4m+4-4m+12=m^2-8m+16\)
Để (d) cắt (P) tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow m^2-8m+16>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
mà \(\left(m-4\right)^2\ge0\forall m\)
nên \(m-4\ne0\)
hay \(m\ne4\)
Vậy: khi \(m\ne4\) thì (d) cắt (P) tại hai điểm phân biệt
Đúng 1
Bình luận (0)
Cho hàm số bậc ba yf(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng...
Đọc tiếp
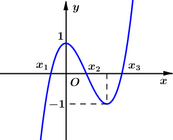
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng
A. 
.
B. 
.
C. 
.
D. 
.
Biết đồ thị hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là
x
1
,
x
2
,
x
3
.
Tính giá trị của biểu thức
T...
Đọc tiếp
Biết đồ thị hàm số f x = a x 3 + b x 2 + c x + d cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là x 1 , x 2 , x 3 . Tính giá trị của biểu thức T = 1 f ' x 1 + 1 f ' x 2 + 1 f ' x 3 .
A. T = 1 3
B. T = 3
C. T = 1
D. T = 0
Đáp án D
Vì x 1 , x 2 , x 3 là ba nghiệm của phương trình f x = 0 ⇒ f x = a x − x 1 x − x 2 x − x 3 .
Ta có f ' x = a x − x 1 x − x 2 x − x 3 + a x − x 2 x − x 3 + a x − x 3 x − x 1 .
Khi đó
f ' x 1 = a x 1 − x 2 x 1 − x 3 f ' x 2 = a x 2 − x 3 x 2 − x 1 f ' x 3 = a x 3 − x 1 x 3 − x 2 ⇒ T = 1 a x 1 − x 2 x 1 − x 3 + 1 a x 2 − x 3 x 2 − x 1 + 1 a x 3 − x 1 x 3 − x 2 = 1 a x 1 − x 2 x 1 − x 3 − 1 a x 1 − x 2 x 2 − x 3 + 1 a x 1 − x 3 x 2 − x 3 = x 2 − x 3 − x 1 + x 3 + x 1 − x 2 a x − x 1 x − x 2 x − x 3 = 0.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
6
x
2
+
4
x
-
7
. Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là
x
1
,
x...
Đọc tiếp
Cho hàm số y = x 3 - 6 x 2 + 4 x - 7 . Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là x 1 , x 2 . Khi đó, giá trị của tổng x 1 + x 2 là
A. -6
B. -4
C. 6
D. 4
Chọn D
x 1 , x 2 là hai nghiệm của phương trình y ' = 0
Khi đó, theo định lý Viet, ta có: x 1 + x 2 = 4 .
Đúng 0
Bình luận (0)
Cho hàm số y 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng? A. (x1 – x2)2 8 B. x1x2 2 C. x2 – x1 3 D. x12 + x22 6
Đọc tiếp
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Đáp án C.
TXĐ: D = R.
Ta có y’ = 6x2 + 6x - 12, y’ = 0 ó 6x2 + 6x – 12 = 0 ó x = 1 hoặc x = -2.
y’’ = 12x + 12, y’’(1) = 24 > 0 => x2 = 1 là điểm cực tiểu, y’’(-2) = -12 < 0 => x1 - 2 là điểm cực đại.
Vậy ta có x2 – x1 = 3.
Đúng 0
Bình luận (0)
Biết rằng đồ thị của hàm số
y
P
x
x
3
−
2
x
2
−
5
x
+
2
cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là
x
1
,
x
2
,
x
3
. Khi đó giá trị của biểu thức
T...
Đọc tiếp
Biết rằng đồ thị của hàm số y = P x = x 3 − 2 x 2 − 5 x + 2 cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là x 1 , x 2 , x 3 . Khi đó giá trị của biểu thức T = 1 x 1 2 − 4 x 1 + 3 + 1 x 2 2 − 4 x 2 + 3 + 1 x 3 2 − 4 x 3 + 3 bằng
A. T = 1 2 − P ' 1 P 1 + P ' 3 P 3
B. T = 1 2 − P ' 1 P 1 − P ' 3 P 3
C. T = 1 2 P ' 1 P 1 − P ' 3 P 3
D. T = 1 2 P ' 1 P 1 + P ' 3 P 3
Đáp án C
Ta có: T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3
T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3 vì 1 x − 1 x − 3 = 1 x − 3 − 1 x − 1 .
Vì x 1 , x 2 , x 3 là 3 nghiệm của phương trình P x = 0 ⇒ P x = x − x 1 x − x 2 x − x 3 .
Suy ra P ' x = x − x 1 x − x 2 + x − x 2 x − x 3 + x − x 3 x − x 1
⇒ P ' x P x = x − x 1 x − x 2 + x − x 3 + x − x 3 x − x 1 x − x 1 x − x 2 x − x 3 = 1 x − x 1 + 1 x − x 2 + 1 x − x 3 * .
Thay x = 1 , x = 3 vào biểu thức (*), ta được T = 1 2 P ' x P 1 − P ' 3 P 3 .
Đúng 0
Bình luận (0)
Cho các số thực
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
0
x
1
x
2
x
3
x
4
và hàm số yf(x). Biết hàm số yf’(x) có đồ thị như hình vẽ. Gọi M và m lần...
Đọc tiếp
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
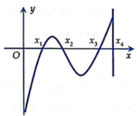
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
