Số nghiệm của phương trình 2 e x + 2018 + 1 1 - x + 1 2 - x + 1 3 - x + 1 4 - x = 0 là
A. 5
B. 1
C. 4
D. 2018
xác định số nghiệm của phương trình |x| + |x+1| +....+|x+2018|=x^2+2018x-2019
em cần gấp ạ
1. Cho phương trình : x² - 2mx + m² -m+1=0 (1) (m là tham số)
Tìm m để phương trình (1) có 2 nghiệm x1,x2 khi đó tìm GTNN của S=(x-x2+2)+x2(x2-x+2)+2018.
\(\Delta=\left(-2m\right)^2-4\left(m^2-m+1\right)\)
=4m^2-4m^2+4m-4=4m-4
Để (1) có 2 nghiệm thì 4m-4>=0
=>m>=1
Cho phương trình: x2 - (2m +3 )x + 4m +2 = 0 (1) với m là tham số
a) Tìm m để phương trình (1) có 1 nghiệm bằng x = 2018 - \(\sqrt{2019}\)
b) Tìm m để phương trình (1) có 2 nghiệm thỏa mãn điều kiện:2x1 - 5x2 = 6
b: \(\text{Δ}=\left(2m+3\right)^2-4\left(4m+2\right)\)
\(=4m^2+12m+9-16m-8\)
\(=4m^2-4m+1=\left(2m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm
Theo đề, ta có:
\(\left\{{}\begin{matrix}2x_1-5x_2=6\\x_1+x_2=2m+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1-5x_2=6\\2x_1+2x_2=4m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x_2=-4m\\2x_1=5x_2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\2x_1=\dfrac{20}{7}m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\x_1=\dfrac{10}{7}m+3\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=4m+2\)
\(\Rightarrow4m+2=\dfrac{40}{49}m^2+\dfrac{12}{7}m\)
\(\Leftrightarrow m^2\cdot\dfrac{40}{49}-\dfrac{16}{7}m-2=0\)
\(\Leftrightarrow40m^2-112m-98=0\)
\(\Leftrightarrow40m^2-140m+28m-98=0\)
=>\(20m\left(2m-7\right)+14\left(2m-7\right)=0\)
=>(2m-7)(20m+14)=0
=>m=7/2 hoặc m=-7/10
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là:
A. 2016.
B. 2017.
C. 2018.
D. Vô số.
Đáp án A.
+ Điều kiện: x > 0
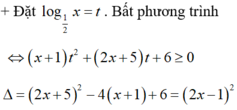
Bất phương trình
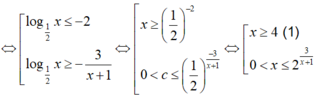
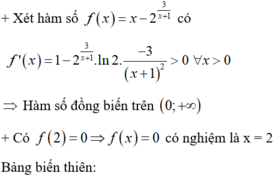
=> Bất phương trình x ≤ 2 3 x + 1 ⇔ f ( x ) ≤ 0 ⇔ 0 < x ≤ 2 ( 2 ) .
Từ (1) và (2) => Tập nghiệm của bất phương trình là
S = ( 0 ; 2 ] ∪ [ 4 ; + ∞ ) .
Vậy có 2016 nghiệm nguyên thỏa mãn.
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là
A. 2016
B. 2017
C. 2018
D. Vô số
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là:
A. 2016
B. 2017
C. 2018
D. Vô số
Đáp án A.
+ Điều kiện: x > 0
+ Đặt log 1 2 x = t . Bất phương trình ⇔ x + 1 t 2 + 2 x + 5 t + 6 ≥ 0
Δ = 2 x + 5 2 − 4 x + 1 + 6 = 2 x − 1 2
Bất phương trình
⇔ log 1 2 x ≤ − 2 log 1 2 x ≥ − 3 x + 1 ⇔ x ≥ 1 2 − 2 0 < c ≤ 1 2 − 3 x + 1 ⇔ x ≥ 4 (1) 0 < x ≤ 2 3 x + 1
+ Xét hàm số f x = x − 2 3 x + 1 có f ' x = 1 − 2 3 x + 1 . ln 2. − 3 x + 1 2 > 0 ∀ x > 0
Hàm số đồng biến trên 0 ; + ∞
+ Có f 2 = 0 ⇒ f x = 0 coa nghiệm là x=2
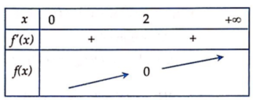
Bảng biến thiên:
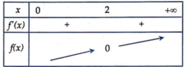
Bất phương trình x ≤ 2 3 x + 1 ⇔ f x ≤ 0 ⇔ 0 < x ≤ 2 ( 2 )
Từ (1) và (2) => Tập nghiệm của bất phương trình là S = 0 ; 2 ∪ 4 ; + ∞
Vậy có 2016 nghiệm nguyên thỏa mãn.
Tìm tất cả các giá trị thực của tham số m để phương trình 5 x 2 + 12 x + 16 = m ( x + 2 ) x 2 + 2 có hai nghiệm thực phân biệt thỏa mãn điều kiện 2017 2 x + x + 1 - 2017 2 x - x + 1 + 2018 x ≤ 2018
A. m ∈ ( 2 6 ; 3 3 ]
B. m ∈ [ 2 6 ; 3 3 ]
C. m ∈ ( 3 3 ; 11 3 3 ) ∪ { 2 6 }
D. m ∈ ( 2 6 ; 11 3 3 )
n là số tự nhiên thỏa mãn phương trình 3 x − 3 − x = 2 cos n x có 2018 nghiệm. Tìm số nghiệm của phương trình: 9 x + 9 − x = 4 + 2 c os 2 n x
A. 4036
B. 4035
C. 2019
D. 2018
Đáp án A
Ta có 9 x + 9 − x − 2 = 2 1 + c os2nx ⇔ 3 x − 3 − x 2 = 4 c os 2 n x ⇔ 3 x − 3 − x = 2 cos n x a 3 x − 3 − x = − 2 cos n x b
Nhận xét x1 là nghiệm của P T a ⇒ − x 1 là nghiệm PT(b)
Giả sử 2PT a ; b có chung nghiệm x0 khi đó 3 x 0 − 3 − x 0 = 2 cos n x 0 3 − x 0 − 3 x 0 = 2 cos n x 0
⇔ 3 x 0 − 3 − x 0 = 2 cos n x 0 3 − x 0 − 3 x 0 = − 2 cos n x 0 ⇒ 3 x 0 = 3 − x 0 ⇒ x 0 = 0 thay vào PT a 3 0 − 3 0 = − 2 c os 0 ⇒ 0 = 1 vô lý
PT (a); (b) không có nghiệm chung. PT có 2.2018 = 4036 nghiệm.
Cho phương trình \(x^2-\left(n-2\right)x-3\) ( n là tham số). Chứng minh phương trình luôn có hai nghiệm \(x_1;x_2\) với mọi n. Tìm n để các nghiệm thoả mãn hệ thức:
\(\sqrt{x^2_1+2018}-x_1=\sqrt{x^2_2+2018}+x_2\)
\(\Delta=\left(n-2\right)^2+12>0\) ; \(\forall n\Rightarrow\) pt đã cho luôn có 2 nghiệm pb trái dấu với mọi n
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=n-2\\x_1x_2=-3\end{matrix}\right.\)
\(\sqrt{x_1^2+2018}-x_2=\sqrt{x_2^2+2018}+x_1\)
\(\Rightarrow x_1^2+x_2^2-2x_2\sqrt{x_1^2+2018}=x_1^2+x_2^2+2018+2x_1\sqrt{x_2^2+2018}\)
\(\Rightarrow-x_2\sqrt{x_1^2+2018}=x_1\sqrt{x_2^2+2018}\)
\(\Rightarrow x_2^2\left(x_1^2+2018\right)=x_1^2\left(x_2^2+2018\right)\)
\(\Rightarrow x_1^2=x_2^2\Rightarrow x_1=-x_2\) (do \(x_1;x_2\) trái dấu)
\(\Rightarrow x_1+x_2=0\Rightarrow n-2=0\Rightarrow n=2\)
Thử lại với \(n=2\) thấy đúng. Vậy...
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
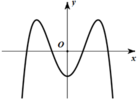
A. 4
B. 0
C. 3
D. 2