Chứng minh rằng hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
a) Cho hàm số y = f(x) = \(3x^2+2\). Chứng minh rằng với mọi x thì f(-x) = f(x)
b)Cho hàm số y= f(x) = \(4x^3-2x.\)Chứng minh rằng với mọi x thì f(-x) = -f(x)
a) \(y=f\left(x\right)=3\left(x^2+\frac{2}{3}\right)\)
\(f\left(-x\right)=3\left[\left(-x\right)^2+\frac{2}{3}\right]=f\left(x\right)^{\left(đpcm\right)}\)
b) Đề sai,thay x = 3 vào là thấy.
Cho hàm số f(x)=\(3x^2+1\)Chứng minh rằng: f(x+1) - f(x) là hàm số bậc nhất
cho hàm số y=f(x)=2.x^2
chứng minh rằng f(x)=f(-x)
giúp mình với sắp kiểm tra học kì rồi
Ta có :
f(-x) = 2 . ( -x )2 = 2x2
Mà f(x) = 2x2
Vậy f(-x) = f(x)
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
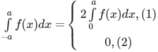
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính:
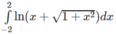
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
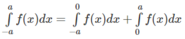
Đổi biến x = - t đối với tích phân
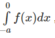
Ta được:
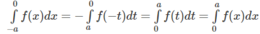
Vậy
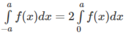
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì 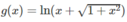
là hàm số lẻ trên đoạn [-2; 2] nên 
Cho hàm số f(x) = 10x
a) Chứng minh rằng f(a + b) = f(a) + f(b)
b) Tìm x sao cho f(x) = \(x^{2}\)
a: f(a+b)=10a+10b
f(a)+f(b)=10a+10b
Do đó: f(a+b)=f(a)+f(b)
Cho hàm số y = f(x) = 4 - 2/5x với x ∈ R. Chứng minh rằng hàm số đã cho nghịch biến trên R.
Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.
cho hàm số y= f(-a)=2.x mũ 3 . Chứng minh rằng f(-a)=-f(a)
Chứng minh rằng hàm số f(x) cho bởi
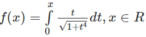
là hàm số chẵn.
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
tick rồi mk giải chi tiết cho
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0